题目内容
10.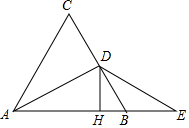 如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H.
如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H.(1)求∠BAD和∠BDE的度数;
(2)求证:点H是AE的中点.
分析 (1)根据等腰三角形的三线合一,可得∠DAB=30°,根据∠ABC=60°,BD=BE,推出∠E=30°.
(2)要证M是BE的中点,根据题意可知,证明△BDE△为等腰三角形,利用等腰三角形的高和中线向重合即可得证.
解答 (1)解:∵在等边△ABC,且D是AC的中点,
∴∠DAB=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×60°=30°,∠ABC=60°,
∵BE=BD,
∴∠BDE=∠E,
∵∠ABC=∠BDE+∠E,
∴∠BDE=∠E=30°,
∴∠BAD=30°,∠BDE=30°.
(2)证明:由(1)可知,∠DAB=∠E=30°
∴AD=ED,△ADE为等腰三角形,
又∵DH⊥AE,
∴H是AE的中点.
点评 本题考查了等腰三角形顶角平分线、底边上的中线和高三线合一的性质以及等边三角形每个内角为60°的知识.辅助线的作出是正确解答本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
20.太仓港区某企业2013年收入2500万元,2015年收入3600万元.
(1)求2013年至2015年该企业收入的年平均增长率;
(2)根据(1)所得的平均增长率,预计2016年该企业收入多少万元?
(1)求2013年至2015年该企业收入的年平均增长率;
(2)根据(1)所得的平均增长率,预计2016年该企业收入多少万元?
18.多项式4x2y-5x3y2+7xy3-6的次数是( )
| A. | 4 | B. | 5 | C. | 3 | D. | 2 |
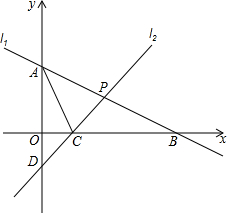 如图,已知直线l1:y=kx+b与x轴和y轴交于点A和点B,直线12:y=x-2与x轴和y 轴分别交于点C和点D,AO=2OC,直线l1和直线l2相交于点P,点P的坐标(4,a),连接 AC.
如图,已知直线l1:y=kx+b与x轴和y轴交于点A和点B,直线12:y=x-2与x轴和y 轴分别交于点C和点D,AO=2OC,直线l1和直线l2相交于点P,点P的坐标(4,a),连接 AC.