题目内容
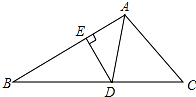 如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则边AC的长是( )
如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则边AC的长是( )| A、3 | B、4 | C、5 | D、6 |
考点:角平分线的性质
专题:
分析:根据角平分线性质求出DF,根据三角形面积公式求出△ABD的面积,求出△ADC面积,即可求出答案.
解答: 解:过D作DF⊥AC于F,
解:过D作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∵S△ADB=
AB×DE=
×5×2=5,
∵△ABC的面积为9,
∴△ADC的面积为9-5=4,
∴
AC×DF=4,
∴
AC×2=4,
∴AC=4
故选B.
 解:过D作DF⊥AC于F,
解:过D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,
∴DE=DF=2,
∵S△ADB=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC的面积为9,
∴△ADC的面积为9-5=4,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴AC=4
故选B.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
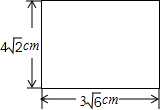 如图,已知一块矩形木板的长和宽分别为3
如图,已知一块矩形木板的长和宽分别为3| 6 |
| 2 |
已知方程组
的解是方程x+y=5的一个解,则m=( )
|
| A、-2 | B、-1 | C、1 | D、2 |
小明同学用10元钱购买两种不同的贺卡共8张,单价分别是1元和2元.设1元的贺卡买了x张,2元的贺卡买了y张,由题意可得方程组为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|

 如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为
如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为 如图,在△ABC中,AB=AC=3cm,△BCN的周长是5cm,AB的垂直平分线交AC于点N,则BC=
如图,在△ABC中,AB=AC=3cm,△BCN的周长是5cm,AB的垂直平分线交AC于点N,则BC=