题目内容
20.计算:①(-$\frac{1}{30}$)÷($\frac{2}{3}$$-\frac{1}{10}$$+\frac{1}{6}$$-\frac{2}{5}$)
②-23-24×($\frac{1}{12}$-$\frac{5}{6}$+$\frac{3}{8}$)
③-14-(1-0.5)×$\frac{1}{3}$×[2-(-3)2]
④(-$\frac{1}{2}$)2×$\frac{4}{3}$+(-2)3÷|-32|+1.
分析 ①先计算括号内的加减运算,再计算除法;
②先计算乘方和括号内的,再计算乘法,最后计算加法;
③先计算乘方和括号内的,再计算乘法,最后计算加法;
④先计算乘方,再计算乘除,最后计算加减即可得.
解答 解:①原式=(-$\frac{1}{30}$)÷($\frac{20}{30}$-$\frac{3}{30}$+$\frac{5}{30}$-$\frac{12}{30}$)
=(-$\frac{1}{30}$)÷$\frac{1}{3}$
=-$\frac{1}{30}$×3
=-$\frac{1}{10}$;
②原式=-8-24×(-$\frac{3}{8}$)
=-8+9
=1;
③原式=-1-$\frac{1}{2}$×$\frac{1}{3}$×(2-9)
=-1-$\frac{1}{6}$×(-7)
=-1+$\frac{7}{6}$
=$\frac{1}{6}$;
④原式=$\frac{1}{4}$×$\frac{4}{3}$+(-8)÷9+1
=$\frac{1}{3}$-$\frac{8}{9}$+1
=$\frac{4}{9}$.
点评 本题主要考查有理数的混合运算,熟练掌握有理数的混合运算顺序和运算法则是解题的关键.

练习册系列答案
相关题目
15.按要求完成下列问题:
(1)若A、B、C、D、E是平面内不同的5个点,则过这5个点的直线可能有多少条?要求确定出可能的条数,并画出每种情况的一种简图;
(2)平面内有n(n为不小于2的整数)个点,过这n个点最多能作多少条直线?完成下列表格.
(1)若A、B、C、D、E是平面内不同的5个点,则过这5个点的直线可能有多少条?要求确定出可能的条数,并画出每种情况的一种简图;
(2)平面内有n(n为不小于2的整数)个点,过这n个点最多能作多少条直线?完成下列表格.
| 点的个数 | 2 | 3 | 4 | 5 | … | 2016 | … | n |
| 能做直线最多条数 | 1 | 3 | 6 | / | … | 2031120 | … | $\frac{n(n-1)}{2}$ |
5. 如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
 如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )
如图,一个长方形观光园,它的长为100米,宽为50米,在它的四角各建一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)花园种植的是花草,设正方形观光休息亭的边长为x米,则下列说法中错误的是( )| A. | 观光园的周长为300米 | B. | 观光休息亭的占地面积为4x2米2 | ||
| C. | 花园占地面积为(100-2x)(50-2x)米2 | D. | 观光大道总长为(300-2x)米 |
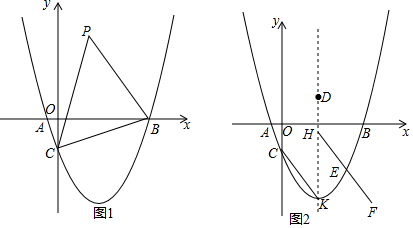
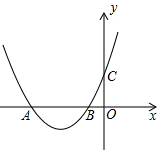 如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.
如图,抛物线y=$\frac{1}{8}$x2+3mx+18m2-m与x轴交于A(x1,0),B(x2,0)两点,且x1≠x2,与y轴交于点C.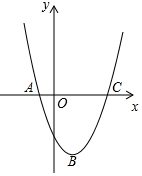 如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),与x轴的另一个交点为C.
如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),与x轴的另一个交点为C.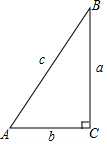 如图,在Rt△ABC中,∠C=90°,若a=4,c=5,则tanA=$\frac{4}{3}$.
如图,在Rt△ABC中,∠C=90°,若a=4,c=5,则tanA=$\frac{4}{3}$.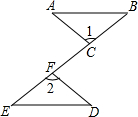 如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你再补充一个条件,使△ABC≌△DEF,你补充的条件是FD=AC(答案不唯一).
如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你再补充一个条件,使△ABC≌△DEF,你补充的条件是FD=AC(答案不唯一).