题目内容
9.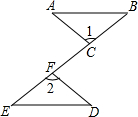 如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你再补充一个条件,使△ABC≌△DEF,你补充的条件是FD=AC(答案不唯一).
如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你再补充一个条件,使△ABC≌△DEF,你补充的条件是FD=AC(答案不唯一).
分析 已知△ABC与△DEF中有一组边与一组角相等,根据全等三角形的判定可知,只需要添加一组边或一组角即可全等.
解答 解:添加FD=AC,
∵BF=EC,
∴BF-CF=EC-CF
∴BC=EF
在△ABC与△DEF中,
$\left\{\begin{array}{l}{BC=EF}\\{∠1=∠2}\\{AC=DF}\end{array}\right.$
∴△ABC≌△DEF(SAS)
故答案为:FD=AC(答案不唯一)
点评 本题考查全等三角形的判定,解题的关键是熟练全等三角形的判定条件,本题属于基础题型.

练习册系列答案
相关题目
4.若点O是△ABC三边垂直平分线的交点,则有( )
| A. | OA=OB≠OC | B. | OB=OC≠OA | C. | OC=OA≠OB | D. | OA=OB=OC |
18.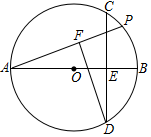 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )| A. | $\frac{\sqrt{3}}{3}$π | B. | $\sqrt{3}$ | C. | $\frac{2}{3}$π | D. | 2 |
19.化简($\sqrt{3}$+1)($\sqrt{3}$-1)+$\sqrt{12}$-$\root{3}{8}$的结果是( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用26米长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x米.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用26米长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x米.