题目内容
19.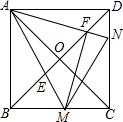 如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.(1)求证:$\frac{AF}{AM}$=$\frac{\sqrt{2}}{2}$;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
分析 (1)先证明A、B、M、F四点共圆,根据圆内接四边形对角互补即可证明∠AFM=90°,根据等腰直角三角形性质即可解决问题.
(2)由(1)的结论即可证明.
(3)由:A、B、M、F四点共圆,推出∠BAM=∠EFM,因为∠BAM=∠FMN,所以∠EFM=∠FMN,推出MN∥BD,得到$\frac{CM}{CB}$=$\frac{CN}{CD}$,推出BM=DN,再证明△ABM≌△ADN即可解决问题.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,∠ABC=90°,
∵∠MAN=45°,
∴∠MAF=∠MBE,
∴A、B、M、F四点共圆,
∴∠ABM+∠AFM=180°,
∴∠AFM=90°,
∴∠FAM=∠FMA=45°,
∴AM=$\sqrt{2}$AF,
∴$\frac{AF}{AM}$=$\frac{\sqrt{2}}{2}$.
补充不用四点共圆的方法:由△EAF∽△EBM,推出$\frac{AE}{BE}$=$\frac{EF}{EM}$,即$\frac{AE}{EF}$=$\frac{BE}{EM}$,即可推出△AEB∽△FEM,推出∠EMF=∠ABE=45°,由此即可解决问题.
(2)由(1)可知∠AFM=90°,
∴AF⊥FM.
(3)结论:∠BAM=22.5时,∠FMN=∠BAM
理由:∵△AEB∽△FEM
∴∠BAE=∠EFM,
∵∠BAM=∠FMN,
∴∠EFM=∠FMN,
∴MN∥BD,
∴$\frac{CM}{CB}$=$\frac{CN}{CD}$,∵CB=DC,
∴CM=CN,
∴MB=DN,
在△ABM和△ADN中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABM=∠ADN=90°}\\{BM=DN}\end{array}\right.$,
∴△ABM≌△ADN,
∴∠BAM=∠DAN,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠BAM=22.5°.
点评 本题考查四边形综合题、等腰直角三角形性质、四点共圆、全等三角形的判定和性质等知识,解题的关键是利用四点共圆的性质解决问题,题目有点难,用到四点共圆.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B. | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C. | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D. | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
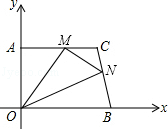 在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为(3,4).
在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为(3,4). 如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.
如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.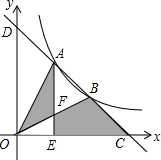 如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.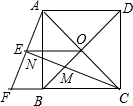 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.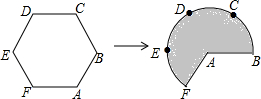 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18.
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=120°.
如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=120°.