题目内容
7. 如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.
如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.
分析 根据从左面看得到的图形是左视图,从前面看的到的视图是主视图,再根据面积求出面积的和即可.
解答 解:该几何体的主视图的面积为1×1×4=4,左视图的面积是1×1×3=3,
所以该几何体的主视图和左视图的面积之和是3+4=7,
故答案为:7.
点评 本题考查了简单几何体的三视图,确定左视图、主视图是解题关键.

练习册系列答案
相关题目
15.下列分式运算,正确的是( )
| A. | ($\frac{2y}{3x}$)2=$\frac{2{y}^{2}}{3{x}^{2}}$ | B. | $\frac{1}{x-y}-\frac{1}{y-x}=0$ | C. | $\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3(x+y)}$ | D. | ($\frac{{x}^{2}}{-y}$)3=$-\frac{{x}^{6}}{{y}^{3}}$ |
12. 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )
 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )| A. |  | B. |  | C. |  | D. |  |
17.A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )
| A. | $\frac{180}{x}$-$\frac{180}{(1+50%)x}$=1 | B. | $\frac{180}{(1+50%)x}$-$\frac{180}{x}$=1 | ||
| C. | $\frac{180}{x}$-$\frac{180}{(1-50%)x}$=1 | D. | $\frac{180}{(1-50%)x}$-$\frac{180}{x}$=1 |
 如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?
如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?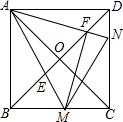 如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.