题目内容
8.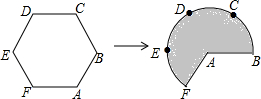 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18.
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18.
分析 由正六边形的性质得出$\widehat{BAF}$的长=12,由扇形的面积=$\frac{1}{2}$弧长×半径,即可得出结果.
解答 解:∵正六边形ABCDEF的边长为3,
∴AB=BC=CD=DE=EF=FA=3,
∴$\widehat{BAF}$的长=3×6-3-3═12,
∴扇形AFB(阴影部分)的面积=$\frac{1}{2}$×12×3=18.
故答案为:18.
点评 本题考查了正多边形和圆、正六边形的性质、扇形面积公式;熟练掌握正六边形的性质,求出弧长是解决问题的关键.

练习册系列答案
相关题目
13.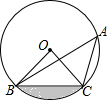 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )| A. | π-4 | B. | $\frac{2}{3}π-1$ | C. | π-2 | D. | $\frac{2π}{3}-2$ |
20.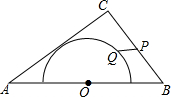 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )| A. | 6 | B. | 2$\sqrt{13}$+1 | C. | 9 | D. | $\frac{32}{2}$ |
17.A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )
| A. | $\frac{180}{x}$-$\frac{180}{(1+50%)x}$=1 | B. | $\frac{180}{(1+50%)x}$-$\frac{180}{x}$=1 | ||
| C. | $\frac{180}{x}$-$\frac{180}{(1-50%)x}$=1 | D. | $\frac{180}{(1-50%)x}$-$\frac{180}{x}$=1 |
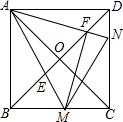 如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.