��Ŀ����
9����������У������ѧ���꼶ѧ��ȥ��ѧУ10ǧ�IJ���ݲιۣ�һ����ѧ�������г����ߣ�����$\frac{1}{3}$Сʱ������ѧ���������������������ͬʱ�ﵽ����֪������ѧ�����ٶ����ﳵѧ���ٶȵ�2�������ﳵѧ�����ٶȣ����ﳵѧ�����ٶ�ΪÿСʱxǧ�ף������з�����ȷ���ǣ�������| A�� | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B�� | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C�� | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D�� | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
���� ��������������ѧ��ʱ���Ϊ$\frac{1}{3}$Сʱ�������ó���ʽ����𰸣�
��� �⣺���ﳵѧ�����ٶ�ΪÿСʱxǧ�ף���������ɵã�
$\frac{10}{x}$=$\frac{10}{2x}$+$\frac{1}{3}$��
��ѡ��A��
���� ������Ҫ��������ʵ������������ʽ���̣���ȷ�ҳ�������ϵ�ǽ���ؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
20�����б�־������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ�������
| A�� |  | B�� |  | C�� |  | D�� |  |
4����-2+��+3��-��-5��+��-4��-��+3��д��ʡ�����ź͵���ʽ����ȷ���ǣ�������
| A�� | -2+3-5-4-3 | B�� | -2+3+5-4+3 | C�� | -2+3+5+4-3 | D�� | -2+3+5-4-3 |
1��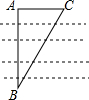 ��ͼ��Ϊ����������A��B���룬����AB��ֱ����ȡ��C�����AC=a����ACB=������A��B����ľ���Ϊ��������
��ͼ��Ϊ����������A��B���룬����AB��ֱ����ȡ��C�����AC=a����ACB=������A��B����ľ���Ϊ��������
 ��ͼ��Ϊ����������A��B���룬����AB��ֱ����ȡ��C�����AC=a����ACB=������A��B����ľ���Ϊ��������
��ͼ��Ϊ����������A��B���룬����AB��ֱ����ȡ��C�����AC=a����ACB=������A��B����ľ���Ϊ��������| A�� | asin�� | B�� | acos�� | C�� | atan�� | D�� | $\frac{a}{tan��}$ |
 ��ͼ��ij����С����һ������¥���ڸ�¥��ǰ��32�״�Ҫ�ٸ�һ��30����¥�������˽���¥�Բɹ��Ӱ�죬�����������������ˮƽ�ߵļн�Ϊ37��ʱ������¥��Ӱ���ھ���¥���ж�ߣ�
��ͼ��ij����С����һ������¥���ڸ�¥��ǰ��32�״�Ҫ�ٸ�һ��30����¥�������˽���¥�Բɹ��Ӱ�죬�����������������ˮƽ�ߵļн�Ϊ37��ʱ������¥��Ӱ���ھ���¥���ж�ߣ�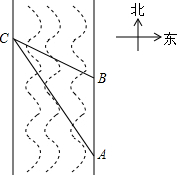 ��һ����ѧʵ���У���ʦ����ѧ��ȥ��һ���ϱ�����ĺӵĿ��ȣ���ͼ��ijͬѧ�ںӶ�����A���۲�Ӷ�ˮ���е�C�����C��A��ƫ��31��ķ����ϣ��غӰ���ǰ��20����B�������C��B��ƫ��45��ķ����ϣ��������ӵĿ���30�ף����ο����ݣ�$tan31��=\frac{3}{5}��sin31���\frac{1}{2}$��
��һ����ѧʵ���У���ʦ����ѧ��ȥ��һ���ϱ�����ĺӵĿ��ȣ���ͼ��ijͬѧ�ںӶ�����A���۲�Ӷ�ˮ���е�C�����C��A��ƫ��31��ķ����ϣ��غӰ���ǰ��20����B�������C��B��ƫ��45��ķ����ϣ��������ӵĿ���30�ף����ο����ݣ�$tan31��=\frac{3}{5}��sin31���\frac{1}{2}$��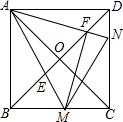 ��ͼ��������ABCD�ĶԽ����ཻ�ڵ�O����M��N�ֱ��DZ�BC��CD�ϵĶ��㣨�����B��C��D�غϣ���AM��AN�ֱ�BD�ڵ�E��F���ҡ�MANʼ�ձ���45�㲻�䣮
��ͼ��������ABCD�ĶԽ����ཻ�ڵ�O����M��N�ֱ��DZ�BC��CD�ϵĶ��㣨�����B��C��D�غϣ���AM��AN�ֱ�BD�ڵ�E��F���ҡ�MANʼ�ձ���45�㲻�䣮