题目内容
4.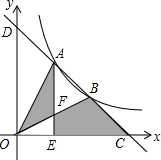 如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.(1)b=m+$\frac{4}{m}$(用含m的代数式表示);
(2)若S△OAF+S四边形EFBC=4,则m的值是$\sqrt{2}$.
分析 (1)根据待定系数法点A的纵坐标相等列出等式即可解决问题.
(2)作AM⊥OD于M,BN⊥OC于N.记△AOF面积为S,则△OEF面积为2-S,四边形EFBC面积为4-S,△OBC和△OAD面积都是6-2S,△ADM面积为4-2S=2(2-s),所以S△ADM=2S△OEF,推出EF=$\frac{1}{2}$AM=$\frac{1}{2}$NB,得B(2m,$\frac{2}{m}$)代入直线解析式即可解决问题.
解答 解:(1)∵点A在反比例函数y=$\frac{4}{x}$(x>0)的图象上,且点A的横坐标为m,
∴点A的纵坐标为$\frac{4}{m}$,即点A的坐标为(m,$\frac{4}{m}$).
令一次函数y=-x+b中x=m,则y=-m+b,
∴-m+b=$\frac{4}{m}$
即b=m+$\frac{4}{m}$.
故答案为:m+$\frac{4}{m}$.
(2)作AM⊥OD于M,BN⊥OC于N.
∵反比例函数y=$\frac{4}{x}$,一次函数y=-x+b都是关于直线y=x对称,
∴AD=BC,OD=OC,DM=AM=BN=CN,记△AOF面积为S,
则△OEF面积为2-S,四边形EFBC面积为4-S,△OBC和△OAD面积都是6-2S,△ADM面积为4-2S=2(2-s),
∴S△ADM=2S△OEF,
由对称性可知AD=BC,OD=OC,∠ODC=∠OCD=45°,△AOM≌△BON,AM=NB=DM=NC,
∴EF=$\frac{1}{2}$AM=$\frac{1}{2}$NB,
∴EF是△OBN的中位线,
∴N(2m,0),
∴点B坐标(2m,$\frac{2}{m}$)代入直线y=-x+m+$\frac{4}{m}$,
∴$\frac{2}{m}$=-2m+m+$\frac{4}{m}$,整理得到m2=2,
∵m>0,
∴m=$\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查反比例函数与一次函数图象的交点、对称等知识,解题的关键是利用对称性得到很多相等的线段,学会设参数解决问题,属于中考填空题中的压轴题.

| A. | ($\frac{2y}{3x}$)2=$\frac{2{y}^{2}}{3{x}^{2}}$ | B. | $\frac{1}{x-y}-\frac{1}{y-x}=0$ | C. | $\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3(x+y)}$ | D. | ($\frac{{x}^{2}}{-y}$)3=$-\frac{{x}^{6}}{{y}^{3}}$ |
 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )| A. |  | B. |  | C. |  | D. |  |
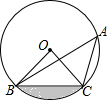 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )| A. | π-4 | B. | $\frac{2}{3}π-1$ | C. | π-2 | D. | $\frac{2π}{3}-2$ |
| A. | a5 | B. | a-5 | C. | a8 | D. | a-8 |
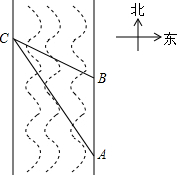 在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)
在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)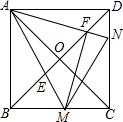 如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.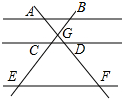 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$.
如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$.