题目内容
15.如图1,在△ABC中,∠A=120°,AB=AC,点P、Q同时从点B出发,以相同的速度分别沿折线B→A→C、射线BC运动,连接PQ.当点P到达点C时,点P、Q同时停止运动.设BQ=x,△BPQ与△ABC重叠部分的面积为S.如图2是S关于x的函数图象(其中0≤x≤8,8<x≤m,m<x≤16时,函数的解析式不同).(1)填空:m的值为8$\sqrt{3}$;
(2)求S关于x的函数关系式,并写出x的取值范围;
(3)请直接写出△PCQ为等腰三角形时x的值.
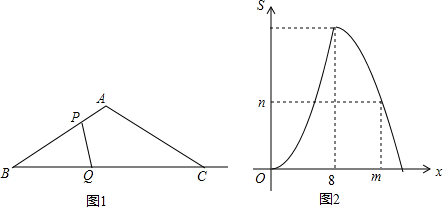
分析 (1)根据题意求出BC的长即可.
(2)分三种情形①0≤m≤8,②8<x≤8$\sqrt{3}$,③8$\sqrt{3}$<x≤16,分别求出△APQ面积即可.
(3)分三种情形讨论①当点P在AB上,点Q在BC上,△PQC不可能为等腰三角形.②当点P在AC上,点Q在BC上,根据PQ=QC列出方程即可③当点P在AC上,点Q在BC的延长线,根据CP=CQ列出方程即可.
解答 解:(1)如图1中,作AM⊥BC,PN⊥BC,垂足分别为M,N.
由题意AB=AC=8,∠A=120°,
∴∠BAM=∠CAM=60°,∠B=∠C=30°,
∴AM=$\frac{1}{2}$AB=4,BM=CM=4$\sqrt{3}$,
∴BC= 8$\sqrt{3}$,
8$\sqrt{3}$,
∴m=BC=8$\sqrt{3}$,
故答案为8$\sqrt{3}$.
(2)①当0≤m≤8时,如图1中,
在RT△PBN中,∵∠PNB=90°,∠B=30°,PB=x,
∴PN=$\frac{1}{2}$x.
s=$\frac{1}{2}$•BQ•PN=$\frac{1}{2}$•x•$\frac{1}{2}$•x=$\frac{1}{4}$x2.
②当8<x≤8$\sqrt{3}$,如图2中,
在RT△PBN中,∵PC=16-x,∠PNC=90°,∠C=30°,
∴PN=$\frac{1}{2}$PC=8-$\frac{1}{2}$x,
∴s=$\frac{1}{2}$•BQ•PN=$\frac{1}{2}$•x•(8-$\frac{1}{2}$x)=-$\frac{1}{4}$x2+4x.
③当8$\sqrt{3}$<x≤16时,
s=$\frac{1}{2}$•8$\sqrt{3}$•(8-$\frac{1}{2}$•x)=-2$\sqrt{3}$x+32$\sqrt{3}$.
(3)①当点P在AB上,点Q在BC上时,△PQC不可能是等腰三角形.
②当点P在AC上,点Q在BC上时,PQ=QC,
∵PC=$\sqrt{3}$QC,
∴16-x=$\sqrt{3}$(8$\sqrt{3}$-x),
∴x=4$\sqrt{3}$+4.
③当点P在AC上,点Q在BC的延长线时,PC=CQ,
即16-x=x-8$\sqrt{3}$,
∴x=8+4$\sqrt{3}$.
∴△PCQ为等腰三角形时x的值为4$\sqrt{3}$+4或8+4$\sqrt{3}$.
点评 本题考查动点问题、等腰三角形的判定和性质、三角形的面积等知识,解题的关键是读懂图象信息,学会分类讨论的思想,属于中考常考题型.

| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
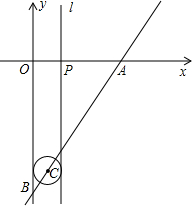 如图,平面直角坐标系的单位是厘米,直线AB的解析式为y=$\sqrt{3}$x-6$\sqrt{3}$分别与x轴、y轴相交于A、B两点.点C沿射线BA以3厘米/秒的速度运动,以点C为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,运动时间为t(t>0),过点P作直线l垂直于x轴.
如图,平面直角坐标系的单位是厘米,直线AB的解析式为y=$\sqrt{3}$x-6$\sqrt{3}$分别与x轴、y轴相交于A、B两点.点C沿射线BA以3厘米/秒的速度运动,以点C为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,运动时间为t(t>0),过点P作直线l垂直于x轴. 如图,AB∥CD,∠B=53°,∠C=35°,求∠CDE和∠A的度数.
如图,AB∥CD,∠B=53°,∠C=35°,求∠CDE和∠A的度数.