题目内容
3.已知方程组$\left\{\begin{array}{l}{x-2y=1}\\{x+2y=n}\end{array}\right.$和$\left\{\begin{array}{l}{x+y=m}\\{2x-3y=5}\end{array}\right.$的解相同,(1)求m,n的值.
(2)求方程组的解.
分析 (1)根据方程组解的定义先求出方程组的解,再求出m、n的值.
(2)方程组$\left\{\begin{array}{l}{x-2y=1}\\{2x-3y=5}\end{array}\right.$的解就是原来方程组的解.
解答 解:(1)∵方程组$\left\{\begin{array}{l}{x-2y=1}\\{x+2y=n}\end{array}\right.$和$\left\{\begin{array}{l}{x+y=m}\\{2x-3y=5}\end{array}\right.$的解相同,
∴方程组$\left\{\begin{array}{l}{x-2y=1}\\{2x-3y=5}\end{array}\right.$的解$\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$是上面两个方程组的解,
∴m=x+y=10,n=x+2y=13,
(2)由(1)可知方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$.
点评 本题考查二元一次方程组的解,正确理解方程组解的定义是解决问题的关键,知道方程组$\left\{\begin{array}{l}{x-2y=1}\\{2x-3y=5}\end{array}\right.$的解就是原方程组的解,属于中考常考题型.

练习册系列答案
相关题目
9. 在平面直角坐标系中,正方形的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
在平面直角坐标系中,正方形的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
 在平面直角坐标系中,正方形的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
在平面直角坐标系中,正方形的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )| A. | (0,2) | B. | (2,0) | C. | (0,-2) | D. | (-2,0) |
10.下列命题的逆命题不正确的是( )
| A. | 菱形的四条边都相等 | B. | 两直线平行,内错角相等 | ||
| C. | 等腰三角形的两个底角相等 | D. | 全等三角形的对应角相等 |
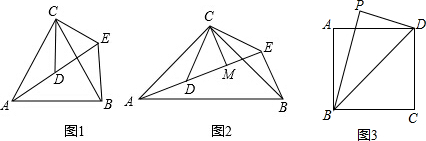
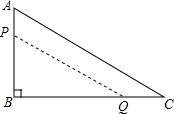 如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.
如图,在ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动,动点Q从点B开始沿边BC向C以4mm/s的速度移动,如果P、Q分别从A、B同时出发,那么PBQ的面积S随出发时间t如何变化?写出函数关系式及t的取值范围.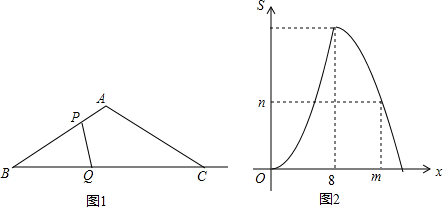
 如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长=9.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长=9.