题目内容
4. 如图,AB∥CD,∠B=53°,∠C=35°,求∠CDE和∠A的度数.
如图,AB∥CD,∠B=53°,∠C=35°,求∠CDE和∠A的度数.
分析 由AB∥CD可知∠CDE=∠B,再由∠BDC与∠CDE互补可求出∠BDC的度数,根据四边形的内角为360°可算出∠A的度数.
解答 解:∵AB∥CD,
∴∠CDE=∠B=53°.
∵∠BDC+∠CDE=180°,
∴∠BDC=127°,
∵四边形的内角和为360°,
∴∠A=360°-∠B-∠C-∠BDC=145°.
点评 本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质找出角之间的关系.本题属于基础题,难度不大,解决该类型题目时,根据平行线的性质找出相等或互补的量即可.

练习册系列答案
相关题目
10.下列命题的逆命题不正确的是( )
| A. | 菱形的四条边都相等 | B. | 两直线平行,内错角相等 | ||
| C. | 等腰三角形的两个底角相等 | D. | 全等三角形的对应角相等 |
9.若$\sqrt{{a}^{2}}=(\sqrt{a})^{2}$,则a的取值范围是( )
| A. | a≥0 | B. | a≠0 | C. | a<0 | D. | a为任意实数 |
16.下列计算正确的是( )
| A. | (-a3)4=a12 | B. | a3•a4=a12 | C. | 3a•4a=12a | D. | (a3)2=a9 |
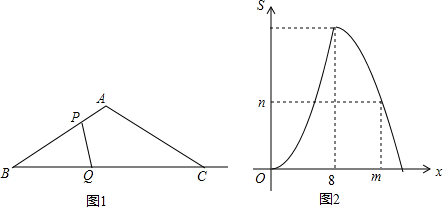
 如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长=9.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,则线段AC的长=9.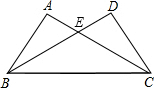 如图,AC与BD交于点E,AB=DC,∠ABC=∠DCB.若∠DBC=35°,求∠ACB的度数.
如图,AC与BD交于点E,AB=DC,∠ABC=∠DCB.若∠DBC=35°,求∠ACB的度数.