计算:(1)$$, (2)$\sqrt{300}-\sqrt{48}$．题目和参考答案——青夏教育精英家教网—

题目内容

7．计算：
（1）$（\sqrt{11}+2\sqrt{3}）（2\sqrt{3}-\sqrt{11}）$；
（2）$\sqrt{300}-\sqrt{48}$．

分析（1）直接利用平方差公式求出答案；
（2）首先化简二次根式进而合并求出答案．

解答解：（1）$（\sqrt{11}+2\sqrt{3}）（2\sqrt{3}-\sqrt{11}）$
=（2$\sqrt{3}$）²-（$\sqrt{11}$）²
=12-11
=1；

（2）$\sqrt{300}-\sqrt{48}$
=10$\sqrt{3}$-4$\sqrt{3}$
=6$\sqrt{3}$．

点评此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．

练习册系列答案

14．（1）问题发现
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．
填空：
①∠AEB的度数为60°；
②线段AD、BE之间的数量关系为AD=BE．
（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．
（3）解决问题
如图3，在正方形ABCD中，CD=2，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．

15．如图1，在△ABC中，∠A=120°，AB=AC，点P、Q同时从点B出发，以相同的速度分别沿折线B→A→C、射线BC运动，连接PQ．当点P到达点C时，点P、Q同时停止运动．设BQ=x，△BPQ与△ABC重叠部分的面积为S．如图2是S关于x的函数图象（其中0≤x≤8，8＜x≤m，m＜x≤16时，函数的解析式不同）．
（1）填空：m的值为8$\sqrt{3}$；
（2）求S关于x的函数关系式，并写出x的取值范围；
（3）请直接写出△PCQ为等腰三角形时x的值．

2．

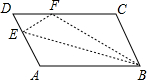如图，平行四边形ABCD中，点E在边AD上，以BE为折痕，将△ABE折叠，使点A正好与CD上的F点重合，若△FDE的周长为16，△FCB的周长为28，则FC的长为6．

12．计算
（1）${（-1）^{2013}}+6×（{\frac{1}{3}-\frac{1}{2}}）+{（{\sqrt{2}-2}）^0}$
（2）$|{-\sqrt{3}}|-\sqrt{12}+tan{60°}+{（{\frac{1}{3}}）^{-1}}$．

19．已知$\frac{a}{b}$=$\frac{2}{3}$，那么$\frac{2a-5b}{6a}$=-$\frac{11}{12}$．

（-a³）⁴=a¹²

a³•a⁴=a¹²

（a³）²=a⁹

试题分类