题目内容
已知AD是△ABC的底边上高，若AB-BD=AC-CD，求证：△ABC为等腰三角形．
考点：等腰三角形的判定
专题：证明题
分析：根据题意画出图形，通过勾股定理得出等式AB2-BD2=AC2-CD2，与已知等式联立得AB+BD=AC+CD，从而得出最后结果．
解答：证明：∵三角形ABD和ACD是直角三角形，
∴AB2-BD2=AC2-CD2①，
∵AB-BD=AC-CD②，
由①②得：
AB+BD=AC+CD③，
②+③得：
2AB=2AC，
∴AB=AC．
∴△ABC为等腰三角形．
∴AB2-BD2=AC2-CD2①，
∵AB-BD=AC-CD②，
由①②得：
AB+BD=AC+CD③，
②+③得：
2AB=2AC，
∴AB=AC．
∴△ABC为等腰三角形．
点评：本题主要考查了勾股定理的运用，要掌握勾股定理的含义：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
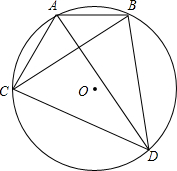如图，AD，BC是圆O的两条相互垂直的弦，AB=2，CD=4，则⊙O的半径为
如图，正方形ABCD的边长为a cm，剪去4个角后成为正八边形，则正八边形的边长为多少？面积为多少？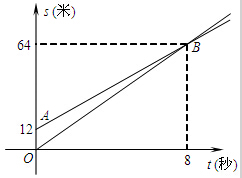
如图，图中两条射线分别表示甲、乙两名同学运动的路程s（米）和时间t（秒）的关系图象，已知甲的速度比乙快．下面么给出四种说法：
如图，数轴上点A表示
如图为二次函数y=ax2+bx+c（a≠0）的图象，下面四条信息：①abc＞0；②4a+c＜2b；③4ac-b2＜0；④3b+2c＜0，其中正确信息的个数是（ ）