题目内容
已知四边形有一个内角为120°,一条对角线把四边形分成一个等边三角形和一个直角三角形,且该对角线长为2,求该四边形的面积.
考点:二次根式的应用
专题:
分析:首先由等边三角形的性质得出∠CAB=60°,AC=BC=AC=2,根据三角形的面积公式求出S△ABC=
AB•(AC•sin∠CAB)=
×2×(2×
)=
.然后在Rt△ADC中,求出∠CAD=∠DAB-∠CAB=60°.再分两种情况进行讨论:①∠D=90°;②如果∠ACD=90°.分别求出S△ADC,再根据S四边形ABCD=S△ABC+S△ADC即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
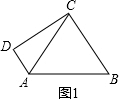
解答:解:如图,四边形ABCD中,∠DAB=120°,AC把四边形分成等边三角形ABC和一个直角三角形ADC,AC=2.
∵三角形ABC中,AC=2,
∴∠CAB=60°,AC=BC=AC=2,
∴S△ABC=
AB•(AC•sin∠CAB)=
×2×(2×
)=
.
 在Rt△ADC中,∠CAD=∠DAB-∠CAB=120°-60°=60°.
在Rt△ADC中,∠CAD=∠DAB-∠CAB=120°-60°=60°.
分两种情况:
①如果∠D=90°,如图1,
∵∠ACD=30°,AC=2,
∴AD=
AC=1,CD=
AD=
,
∴S△ADC=
AD•CD=
×1×
=
,
 ∴S四边形ABCD=S△ABC+S△ADC=
∴S四边形ABCD=S△ABC+S△ADC=
+
=
;
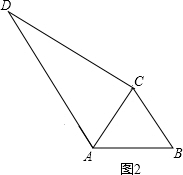
②如果∠ACD=90°,如图2,
∵∠D=30°,AC=2,
∴CD=
AC=2
,
∴S△ADC=
AC•CD=
×2×2
=2
,
∴S四边形ABCD=S△ABC+S△ADC=
+2
=3
.
综上所述,该四边形的面积为
或3
.
∵三角形ABC中,AC=2,
∴∠CAB=60°,AC=BC=AC=2,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
 在Rt△ADC中,∠CAD=∠DAB-∠CAB=120°-60°=60°.
在Rt△ADC中,∠CAD=∠DAB-∠CAB=120°-60°=60°.分两种情况:
①如果∠D=90°,如图1,
∵∠ACD=30°,AC=2,
∴AD=
| 1 |
| 2 |
| 3 |
| 3 |
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
 ∴S四边形ABCD=S△ABC+S△ADC=
∴S四边形ABCD=S△ABC+S△ADC=| 3 |
| ||
| 2 |
3
| ||
| 2 |
②如果∠ACD=90°,如图2,
∵∠D=30°,AC=2,
∴CD=
| 3 |
| 3 |
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S四边形ABCD=S△ABC+S△ADC=
| 3 |
| 3 |
| 3 |
综上所述,该四边形的面积为
3
| ||
| 2 |
| 3 |
点评:本题考查了二次根式的应用,等边三角形、直角三角形的性质,进行分类讨论是解题的关键.

练习册系列答案
相关题目
若点P为直线外一点,点A、B、C、D为直线l上的不同的点,其中PA=3,PB=4,PC=5,PD=3.那么点P到直线1的距离是( )
| A、小于3 | B、3 |
| C、不大于3 | D、不小于3 |
 如图,小正方体的棱长为1,求对角线AG的长.
如图,小正方体的棱长为1,求对角线AG的长. 如图,已知D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.
如图,已知D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数. 如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状.
如图所示,已知∠ABC=∠ADC=90°,AC与BD相交于点P,点E,F分别是AC,BD的中点,判断△EFP的形状. 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.求证:∠BAO=∠CAO.
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.求证:∠BAO=∠CAO. 如图,已知点A是一次函数y=x-4图象上的一点,且矩形ABOC的面积等于3,则点A的坐标为
如图,已知点A是一次函数y=x-4图象上的一点,且矩形ABOC的面积等于3,则点A的坐标为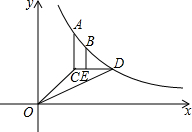 如图,已知反比例函数y=
如图,已知反比例函数y=