题目内容
点O在线段AB上且分AB为1:2两部分(OA<OB),AB=6cm,点M在直线AB上,OM=3OA,则BM= .
考点:两点间的距离
专题:分类讨论
分析:根据线段间的比例关系,可得OA,OB的长OM1,OM2的长,根据线段的和差,可得答案.
解答:解:如图:
 ,
,
点O在线段AB上且分AB为1:2两部分(OA<OB),AB=6cm,
得OA 6×
=2(cm),OB 6-2=4(cm).
由OM=3OA,得
OM1=3OA=6(cm),
由线段的和差得BM1=OM1-OB=6-4=2(cm);
由OM=3OA,得
OM2=3OA=6(cm),
由线段的和差,得
BM2=OM2+OB=6+4=10(cm),故答案为:2cm,或10cm.
 ,
,点O在线段AB上且分AB为1:2两部分(OA<OB),AB=6cm,
得OA 6×
| 1 |
| 3 |
由OM=3OA,得
OM1=3OA=6(cm),
由线段的和差得BM1=OM1-OB=6-4=2(cm);
由OM=3OA,得
OM2=3OA=6(cm),
由线段的和差,得
BM2=OM2+OB=6+4=10(cm),故答案为:2cm,或10cm.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若点P为直线外一点,点A、B、C、D为直线l上的不同的点,其中PA=3,PB=4,PC=5,PD=3.那么点P到直线1的距离是( )
| A、小于3 | B、3 |
| C、不大于3 | D、不小于3 |
 如图,A,B两点的坐标分别是A(1,
如图,A,B两点的坐标分别是A(1, 如图,小正方体的棱长为1,求对角线AG的长.
如图,小正方体的棱长为1,求对角线AG的长.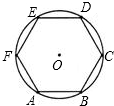 如图,已知正六边形ABCDEF的外接圆半径R=8cm,求四边形ABDE的面积.
如图,已知正六边形ABCDEF的外接圆半径R=8cm,求四边形ABDE的面积. 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.求证:∠BAO=∠CAO.
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.求证:∠BAO=∠CAO.