题目内容
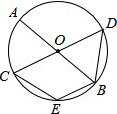已知AB、CD是⊙O的两条直径，CE∥AB，求证： |
| BC |
|
| AE |
|
| AD |
考点：圆心角、弧、弦的关系,圆周角定理
专题：证明题
分析：根据平行线的性质得出弧AC和弧BE相等，即可推出弧AE=弧BC，根据圆心角相等推出弧AD=弧BC，即可得出答案．
解答：证明：∵EC∥AB，
∴弧AC=弧BE，
∴都加上弧EC得：弧AE=弧BC，
∵圆心角AOD=圆心角BOC，
∴弧AD=弧BC，
即
=
=
．
∴弧AC=弧BE，
∴都加上弧EC得：弧AE=弧BC，
∵圆心角AOD=圆心角BOC，
∴弧AD=弧BC，
即
|
| BC |
|
| AE |
|
| AD |
点评：本题考查了平行线的性质，圆心角、弧、弦之间的关系的应用，主要考查学生运用定理进行推理的能力．
练习册系列答案
相关题目
如图，已知D、E分别为AB、AC上的点，AC=BC=BD，AD=AE，DE=CE，求∠B的度数．
如图，在平面直角坐标系内，半径为t的圆D与x轴交于点A（1，0），B（5，0），点D在第一象限，点C的坐标为（0，-2）．
如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于点O，OB=OC．求证：∠BAO=∠CAO．把抛物线y=-x2向右平移一个单位，再向上平移3个单位，得到抛物线的解析式为（ ）
| A、y=-（x-1）2+3 |
| B、y=（x-1）2+3 |
| C、y=-（x+1）2+3 |
| D、y=（x+1）2+3 |