题目内容
1.如果长度分别为a-2,a,a+2的三条线段能组成一个三角形,求a可取的最小整数.分析 根据三角形的三边关系列出不等式,然后确定a的最小整数解即可.
解答 解:由三角形的三边关系可得:a+2-(a-2)<a<a+2+a-2,
解得:a>4,
故a的最小整数解为5.
点评 本题考查了三角形的三边关系,能够确定a的取值范围是解答本题的关键,难度不大.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
9.当x=-2时,2x3+2x2-ax-8=0,则当x=2时,2x3+2x2-ax-8的值为( )
| A. | 0 | B. | -2 | C. | -4 | D. | -8 |
16.若抛物线y=ax2+bx+c与抛物绒y=2x2-4x-1的顶点重合,且与y轴的交点的坐标为(0,1),则抛物线y=ax2+bx+c的表达式是( )
| A. | y=4x2-8x-7 | B. | y=4x2-8x+1 | C. | y=2x2-4x+1 | D. | y=-2x2-4x+1 |
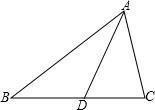 如图,△ABC中,∠BAC=54°,∠B=46°,AD是∠BAC的角平分线,求∠ADC、∠ADB的度数.
如图,△ABC中,∠BAC=54°,∠B=46°,AD是∠BAC的角平分线,求∠ADC、∠ADB的度数.
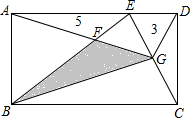 如图,长方形ABCD中,C、G、E在同一条直线上,并且其中有两块小三角形的面积已经标出,求阴影部分的面积.
如图,长方形ABCD中,C、G、E在同一条直线上,并且其中有两块小三角形的面积已经标出,求阴影部分的面积.