题目内容
1.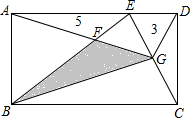 如图,长方形ABCD中,C、G、E在同一条直线上,并且其中有两块小三角形的面积已经标出,求阴影部分的面积.
如图,长方形ABCD中,C、G、E在同一条直线上,并且其中有两块小三角形的面积已经标出,求阴影部分的面积.
分析 由△EBC的面积=矩形面积的一半,△AGD的面积+△GBC的面积=矩形面积的一半,得出S△EBC=S△AGD+S△GBC,得出S△AGD=S△BEG,即可得出阴影部分的面积.
解答 解:根据题意得:${S}_{△EBC}=\frac{1}{2}{S}_{矩形ABCD}$,${S}_{△AGD}+{S}_{△GBC}=\frac{1}{2}{S}_{矩形ABCD}$,
∴S△EBC=S△AGD+S△GBC,
∴S△EBG+S△BCG=S△AGD+S△GBC,
∴S△AGD=S△BEG,
∴S阴影=S△AEF+S△EDG=5+3=8.
点评 本题考查了矩形的性质、三角形面积与矩形面积的关系、阴影部分面积的计算方法;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.甲、乙两人做机械零件,甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求甲、乙每小时各做多少个?若设甲每小时做x个,则可列方程是( )
| A. | $\frac{90}{x-6}=\frac{60}{x}$ | B. | $\frac{90}{x}=\frac{60}{x-6}$ | C. | $\frac{90}{x}=\frac{60}{x+6}$ | D. | $\frac{90}{x+6}=\frac{60}{x}$ |
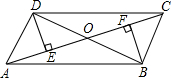 已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF,∠ADB=∠CBD.
已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF,∠ADB=∠CBD.