题目内容
3.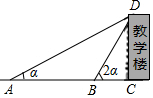 如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.
如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.(1)求教学楼DC的高度;
(2)求cos∠DBC的值.
分析 (1)直接利用锐角三角函数关系得出DC的值;
(2)首先利用外角的性质得出AB=BD,再利用勾股定理得出答案.
解答 解:(1)∵在Rt△ACD中,tanα=$\frac{CD}{AC}$,
∴$\frac{CD}{24}$=$\frac{1}{2}$,
CD=12cm,
答:教学楼DC的高度为12cm;
(2)∵∠DAC=α,∠DBC=2α,
∴∠ADB=∠DAB=α,
∴AB=BD,
设BC=x,则BD=24-x,
故x2+122=(24-x)2,
解得:x=9,
则BD=24-9=15(m),
故cos∠DBC=$\frac{9}{15}$=$\frac{3}{5}$.
点评 此题主要考查了解直角三角形的应用以及勾股定理,正确得出AB=BD是解题关键.

练习册系列答案
相关题目
18.在数学课上,老师提出如下问题:
小云的作法如下:
小云作图的依据是四条边相等的四边形为菱形,菱形的对边平行.
尺规作图:过直线外一点作已知直线的平行线. 已知:直线l及其外一点A. 求作:l的平行线,使它经过点A. |
| (1)在直线l上任取一点B; (2)以B为圆心,BA长为半径作弧,交直线l于点C; 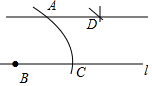 (3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D; (4)作直线AD. 直线AD即为所求. |
 如图,若∠1=∠2=∠3=48°,则∠4=132°.
如图,若∠1=∠2=∠3=48°,则∠4=132°.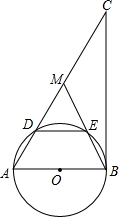 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.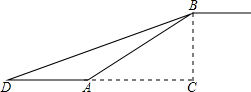 如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).
如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).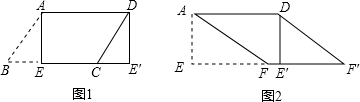
 如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.
如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.