题目内容
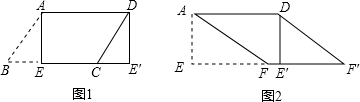
15.(1)如图1所示,平行四边形纸片ABCD中,AD=5,S?ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D是矩形.(2)如图2所示,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
①求证:四边形AFF′D是菱形;
②求四边形AFF′D两条对角线的长.
分析 (1)根据矩形的判定,可得答案;
(2)①根据菱形的判定,可得答案;
②根据勾股定理,可得答案.
解答 解:(1)纸片?ABCD中,AD=5,S?ABCD=15,
过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,
则四边形AEE′D的形状为矩形,
故答案为:矩;
(2)①证明:∵纸片?ABCD中,AD=5,S?ABCD=15,
过点A作AE⊥BC,垂足为E,
∴AE=3.
如图2: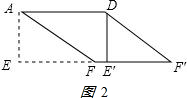 ∵△AEF,将它平移至△DE′F′,
∵△AEF,将它平移至△DE′F′,
∴AF∥DF′,AF=DF′,
∴四边形AFF′D是平行四边形.
在Rt△AEF中,由勾股定理,得
AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AF=AD=5,
∴四边形AFF′D是菱形;
②连接AF′,DF,如图3: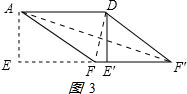
在Rt△DE′F中E′F=FF′-E′F′=5-4=1,DE′=3,
∴DF=$\sqrt{E′{D}^{2}+E′F{′}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
在Rt△AEF′中EF′=EF+FF′=4+5=9,AE=3,
∴AF′=$\sqrt{A{E}^{2}+F′{E}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$.
点评 本题是四边形综合题目,考查了平行四边形的性质、图形的剪拼、矩形的判定,菱形的判定,勾股定理等知识;本题综合性强,有一定难度.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.已知$\left\{\begin{array}{l}{2x+2y=5a}\\{x-4y=1-2a}\end{array}\right.$,且3x-2y=10,a的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
5.下列图形:①等腰三角形;②平行四边形;③菱形;④正六边形;⑤圆.其中既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.
在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.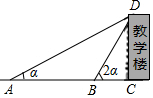 如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.
如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.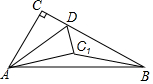 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.