题目内容
13. 如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.
如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.
分析 根据三角形的中位线定理可以证得DE∥BC,则△ADE∽△ABC,根据相似三角形的性质即可求解.
解答 解:∵D、E分别是AB和AC的中点,
∴DE∥BC,且DE=$\frac{1}{2}$BC,即$\frac{DE}{BC}$=$\frac{1}{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{1}{2}$)2=$\frac{1}{4}$,
∵△ABC的面积等于24,
∴△ADE的面积=6.
故答案是:6.
点评 本题考查了三角形中位线定理以及相似三角形的性质定理,理解定理是关键.

练习册系列答案
相关题目
1.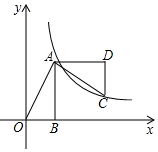 如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
 如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.下列图形:①等腰三角形;②平行四边形;③菱形;④正六边形;⑤圆.其中既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
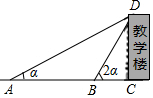 如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.
如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: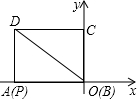 如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),
如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),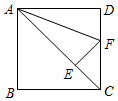 如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.
如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.