题目内容
14.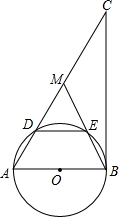 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.(1)求证:∠MDE=∠MED;
(2)填空:
①若AB=6,当DM=2AD时,DE=4;
②连接OD、OE,当∠C的度数为30°时,四边形ODME是菱形.
分析 (1)由于∠ABC=90°,M是AC的中点,BM=AM=MC,从而可知∠A=∠ABM,根据圆内接四边形的性质即可得出∠MDE=∠MED;
(2)①由(1)可知,∠A=∠MDE,由于DE∥AB,所以$\frac{DE}{AB}=\frac{MD}{MA}$,又因为DM=2AD,从而可求出DE的长度;
②当∠C=30°时,此时∠A=60°,所以△AOD是等边三角形,利用等边三角形的性质即可证明OD=OE=EM=DM,从而可知四边形OEMD是菱形.
解答  (1)证明:∵∠ABC=90°,M是AC的中点,
(1)证明:∵∠ABC=90°,M是AC的中点,
∴BM=AM=MC,
∴∠A=∠ABM,
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
又∠ADE+∠MDE=180°,
∴∠MDE=∠MBA,
同理证明:∠MED=∠A,
∴∠MDE=∠MED,
(2)①4,
由(1)可知,∠A=∠MDE,
∴DE∥AB,
∴$\frac{DE}{AB}=\frac{MD}{MA}$
∵DM=2AD,
∴DM:MA=2:3,
∴DE=$\frac{2}{3}$AB=$\frac{2}{3}$×6=4.
②当∠C=30°时,四边形ODME是菱形.
连接OD、OE,
∵OA=OD,∠A=60°,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵DE∥AB,
∴∠ODE=∠AOD=60°,∠MDE=∠MED=∠A=60°,
∴△ODE,△DEM都是等边三角形,
∴OD=OE=EM=DM,
∴四边形OEMD是菱形.
故答案为:(2)①4;②30°
点评 本题考查圆的综合问题,涉及相似三角形的判定与性质,菱形的判定,等边三角形的性质与判定,圆内接四边形的性质,平行线的性质与判定,综合程度较高,需要学生灵活运用所学知识.

练习册系列答案
相关题目
16.下列命题中是真命题的是( )
| A. | 同位角相等 | |
| B. | 有两边及一角分别相等的两个三角形全等 | |
| C. | 两组对边分别相等的四边形是平行四边形 | |
| D. | 垂直于半径的直线是圆的切线 |
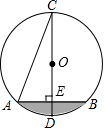 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为$\frac{9}{2}$π-9,.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为$\frac{9}{2}$π-9,. 在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.
在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.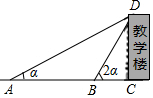 如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.
如图,某中学数学课外学习小组想测量教学楼DC的高度,组员小方在A处仰望教学楼顶端D处,测得∠DAC=α,小方接着向教学楼方向前进到B处,测得∠DBC=2α,已知∠DCA=90°,AC=24m,tanα=$\frac{1}{2}$.