题目内容
9.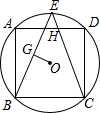 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )| A. | $\frac{1}{8}$ | B. | $\frac{2\sqrt{2}-1}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{\sqrt{2}}{7}$ |
分析 连接AC、BD、DE,根据垂径定理和三角形中位线定理得到DE=2OG=2$\sqrt{2}$,根据勾股定理求出BE,利用△CDH∽△BED和△ACH∽△EDH得到成比例线段,计算即可.
解答 解:连接AC、BD、DE,
∵OG⊥BE,
∴BG=GE,又BO=OD,
∴OG=$\frac{1}{2}$DE,
则DE=2OG=2$\sqrt{2}$,
由勾股定理得,BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=8,
∵∠EBD=∠ECD,∠BED=∠CDH=90°,
∴△CDH∽△BED,
∴$\frac{CD}{BE}$=$\frac{DH}{ED}$,
∴DH=$\frac{CD•ED}{BE}$=$\frac{3\sqrt{2}}{2}$,
∴AH=6-$\frac{3\sqrt{2}}{2}$=$\frac{12-3\sqrt{2}}{2}$,
CH=$\sqrt{C{D}^{2}+D{H}^{2}}$=$\frac{9\sqrt{2}}{2}$,
∵∠CAD=∠DEC,∠ACE=∠ADE,
∴△ACH∽△EDH,
∴$\frac{AH}{EH}$=$\frac{CH}{DH}$,
则EH=$\frac{AH•DH}{CH}$=$\frac{4-\sqrt{2}}{2}$,
∴$\frac{EH}{CH}$=$\frac{2\sqrt{2}-1}{9}$,
故选:B.
点评 本题考查的是圆周角定理、正方形的性质、相似三角形的判定和性质,掌握相关的判定定理和性质定理、正确作出辅助线是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
1.由10个非负整数构成的一组数据x1,x2,…,x10.当它们的平均数、众数、中位数满足下列选项中的哪个时,可以保证x1,x2,…,x10中最大的数据一定不超过7.( )
| A. | 平均数为2,众数为2,中位数为2 | B. | 平均数为3,众数为2,中位数为4 | ||
| C. | 平均数为2,众数为3,中位数为2 | D. | 平均数为2,众数为3,中位数为4 |
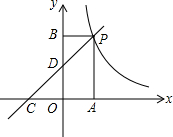 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,S△PBD=2,OA=OC.求:
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,S△PBD=2,OA=OC.求: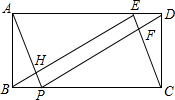 如图,矩形ABCD中,AB=2,BC=5,E、F分别在边AD,BC上,且DE=BP=1.
如图,矩形ABCD中,AB=2,BC=5,E、F分别在边AD,BC上,且DE=BP=1. 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数.
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数. 如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.
如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.