题目内容
1. 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数.
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=140°,请求出∠BFD的度数.
分析 过点E作EG∥AB,根据平行线的性质可得“∠ABE+∠BEG=180°,∠GED+∠EDC=180°”,根据角的计算以及角平分线的定义可得“∠FBE+∠EDF=(∠ABE+∠CDE)÷2=110°”,再依据四边形内角和为360°结合角的计算即可得出结论.
解答 解:过点E作EG∥AB,如图所示.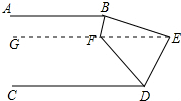
则可得∠ABE+∠BEG=180°,∠GED+∠EDC=180°,
∴∠ABE+∠CDE+∠BED=360°;
又∵∠BED=140°,
∴∠ABE+∠CDE=220°.
∵∠ABE和∠CDE的平分线相交于F,
∴∠FBE+∠EDF=(∠ABE+∠CDE)÷2=110°,
∵四边形的BFDE的内角和为360°,
∴∠BFD=110°.
点评 本题考查了平行线的性质、三角形内角和定理以及四边形内角和为360°,解题的关键是找出∠FBE+∠EDF=110°.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质得出相等(或互补)的角是关键.

练习册系列答案
相关题目
9.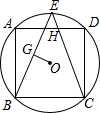 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )| A. | $\frac{1}{8}$ | B. | $\frac{2\sqrt{2}-1}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{\sqrt{2}}{7}$ |
6.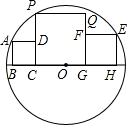 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
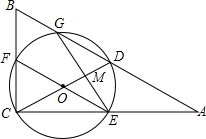 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5. 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则$\widehat{EG}$的长为$\frac{\sqrt{3}π}{6}$.
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则$\widehat{EG}$的长为$\frac{\sqrt{3}π}{6}$. 如图,已知菱形ABCD,AC=8,BD=6,将此菱形绕点A逆时针旋转180°,则该菱形扫过的面积为32π+24.
如图,已知菱形ABCD,AC=8,BD=6,将此菱形绕点A逆时针旋转180°,则该菱形扫过的面积为32π+24.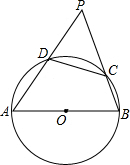 如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P
如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P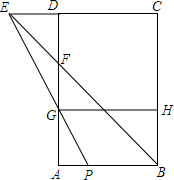 如图,矩形ABCD中,点F在AD上,AF=AB=12,点G是AF的中点,延长CD和BF交于点E,EG的延长线交AB于点P,GH∥AB交BC于点H,已知AP比ED小1.
如图,矩形ABCD中,点F在AD上,AF=AB=12,点G是AF的中点,延长CD和BF交于点E,EG的延长线交AB于点P,GH∥AB交BC于点H,已知AP比ED小1.