题目内容
17.已知关于x的方程(3a+2b)x2+ax+b=0有唯一的解,求这个方程的解.分析 由于(3a+2b)x2+ax+b=0是一元一次方程,于是3a+2b=0,而方程(3a+2b)x2+ax+b=0有唯一解,那么可知a≠0,x=-$\frac{b}{a}$,易得b=-$\frac{3}{2}$a,再代入可求x的值.
解答 解:∵(3a+2b)x2+ax+b=0是一元一次方程,
∴3a+2b=0,
∴b=-$\frac{3}{2}$a,
∵方程(3a+2b)x2+ax+b=0有唯一解,
∴a≠0,x=-$\frac{b}{a}$=-$\frac{-\frac{3}{2}a}{a}$=$\frac{3}{2}$,
即x=$\frac{3}{2}$.
点评 本题考查了一元一次方程的解,解题的关键是理解一元一次方程概念.

练习册系列答案
相关题目
2.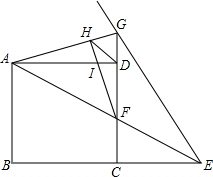 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
①GE+GD=BE;②DG=DF;③AC-2HD=$\sqrt{2}$DF;④当CE=BC=2时,FG=$\frac{5}{3}$.
 如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )
如图,已知正方形ABCD,E为BC延长线上一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G连AG,作FH⊥AG于H,连DH.下列说法正确的是( )①GE+GD=BE;②DG=DF;③AC-2HD=$\sqrt{2}$DF;④当CE=BC=2时,FG=$\frac{5}{3}$.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
9.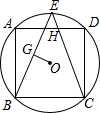 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )| A. | $\frac{1}{8}$ | B. | $\frac{2\sqrt{2}-1}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{\sqrt{2}}{7}$ |
6.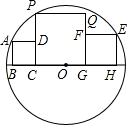 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
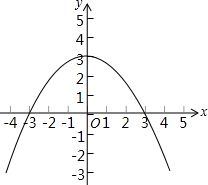 如图,在平面直角坐标系中画出了函数y=ax2+c的图象.
如图,在平面直角坐标系中画出了函数y=ax2+c的图象.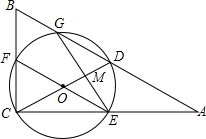 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5.