题目内容
18. 如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.
如图,在直角坐标系中,直线y=-x+4交矩形OACB于F与G,交x轴于D,交y轴于E.(1)△ODE的面积为8;
(2)若∠FOG=45°,求矩形OACB的面积8.
分析 (1)根据一次函数解析式求得OD=OE=4,即可得到结论;
(2)根据等腰直角三角形的性质得到∠ODE=∠OED=45°,推出∠DOF=∠OGE,证得△DOF∽△EGO,根据相似三角形的性质得到DF•EG=OE•OD=16,过点F作FM⊥x轴于点M,过点G作GN⊥y轴于点N.根据勾股定理得到DF=$\sqrt{2}$b,GE=$\sqrt{2}$a,于是得到结论.
解答 解:(1)∵直线y=-x+4与x轴,y轴分别交于点D,点E,
∴D(4,0),E(0,4),
∴OD=OE=4,
∴△ODE的面积=$\frac{1}{2}$OD•OE=$\frac{1}{2}$×4×4=8;
故答案为:8;
(2)∵OD=OE,
∴∠ODE=∠OED=45°;
∴∠OGE=∠ODF+∠DOG=45°+∠DOG,
∵∠EOF=45°,
∴∠DOF=∠EOF++∠DOG=45°+∠DOG,
∴∠DOF=∠OGE,
∴△DOF∽△EGO,
∴$\frac{DF}{OE}$=$\frac{OD}{EG}$,
∴DF•EG=OE•OD=16,
过点F作FM⊥x轴于点M,过点G作GN⊥y轴于点N.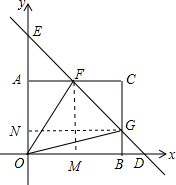 ∴△DMF和△ENG是等腰直角三角形,
∴△DMF和△ENG是等腰直角三角形,
∵NG=AC=a,FM=BC=b,
∴DF=$\sqrt{2}$b,GE=$\sqrt{2}$a,
∴DF•GE=2ab,
∴2ab=16,
∴ab=8,
∴矩形OACB的面积=ab=8.
故答案为8.
点评 本题是一次函数的综合题,考查了一次函数图象上点的坐标特征,三角形相似的判定和性质找出辅助线构建等腰直角三角形,求得DF=$\sqrt{2}$b,GE=$\sqrt{2}$a是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
9.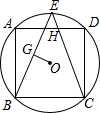 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )| A. | $\frac{1}{8}$ | B. | $\frac{2\sqrt{2}-1}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{\sqrt{2}}{7}$ |
6.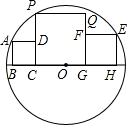 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
 如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )
如图,3个正方形在⊙O直径的同侧,顶点B、C、G、H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上、顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则CG的长为( )| A. | $\frac{12}{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{2}+1$ | D. | 2$\sqrt{2}$ |
 如图,已知菱形ABCD,AC=8,BD=6,将此菱形绕点A逆时针旋转180°,则该菱形扫过的面积为32π+24.
如图,已知菱形ABCD,AC=8,BD=6,将此菱形绕点A逆时针旋转180°,则该菱形扫过的面积为32π+24.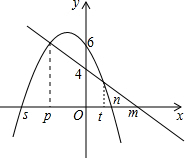 如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).
如图,已知:一次函数图象y1=kx+d与x轴交于点(m,0),与y轴交于(0,4),二次函数y2=ax2+bx+c图象与x轴交于点(s,0)和(n,0),与y轴交于(0,6),且两个函数图象交点的横坐标分别为p、t,则y3=ax2+(b-k)x+2的图象与x轴的交点坐标是(p,0)和(t,0).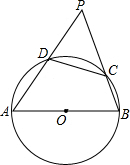 如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P
如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P