题目内容
6.解下列方程:(1)$\frac{x}{x-2}$-1=$\frac{1}{{x}^{2}-4}$;
(2)$\frac{2}{x-2}$+$\frac{8}{4-{x}^{2}}$=0.
分析 (1)方程两边都乘以最简公分母(x2-4),把分式方程化为整式方程,然后求解,再把所求未知数的值代入最简公分母进行检验即可;
(2)方程两边都乘以最简公分母(x2-4),把分式方程化为整式方程,然后求解,再把所求未知数的值代入最简公分母进行检验即可.
解答 解:(1)方程两边都乘以最简公分母(x2-4)得,
x(x+2)-(x2-4)=1,
整理的,2x=-3,
解得x=-$\frac{3}{2}$,
检验:当x=-$\frac{3}{2}$时,x2-4≠0,
所以,x=-$\frac{3}{2}$是原分式方程的根;
(2)方程两边都乘以最简公分母(x2-4)得,
2(x+2)-8=0,
解得x=2,
检验:当x=2时,x2-4=22-4=0,
所以,x=2是分式方程的增根,原方程无解.
点评 本题考查了解分式方程,把分式方程转化为整式方程求解.最后注意需验根.

练习册系列答案
相关题目
16.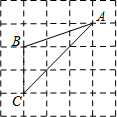 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
如图,△ABC的三个顶点均在格点上,则cosA的值为( )
 如图,△ABC的三个顶点均在格点上,则cosA的值为( )
如图,△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{2\sqrt{5}}{5}$ |
9.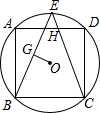 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )| A. | $\frac{1}{8}$ | B. | $\frac{2\sqrt{2}-1}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{\sqrt{2}}{7}$ |