题目内容
14.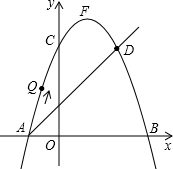 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.(1)试求b、c的值和抛物线顶点F的坐标;
(2)求△ADC的面积;
(3)已知,点Q是直线AD上方抛物线上的一个动点(点Q与A、D不重合),求△AQD的最大面积和此时Q点的坐标.
分析 (1)直接利用待定系数法求出二次函数解析式,进而得出答案;
(2)首先求出直线AD的解析式,进而得出EC的长,利用S△ACD=$\frac{1}{2}×$1×CE+$\frac{1}{2}×$2×CE求出答案;
(3)时候选得出点A、D分别到直线PQ的距离和为3,再利用S△AQD=S△AQP+S△DQP,求出函数最值即可.
解答 解:(1)∵抛物线过A、D,
∴$\left\{\begin{array}{l}{0=-1-b+c}\\{3=-4+2b+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2+2x+3,
∴y=-(x-1)2+4,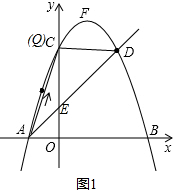 ∴顶点F(1,4);
∴顶点F(1,4);
(2)如图1,∵直线AD也过A、D两点,
∴$\left\{\begin{array}{l}{0=-k+b}\\{3=2k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线AD的解析式为y=x+1,直线AD与y轴的交点E(0,1),
则CE=3-1=2,
∵点A、D分别到y轴的距离为1,2,
∴S△ACD=$\frac{1}{2}×$1×CE+$\frac{1}{2}×$2×CE=3;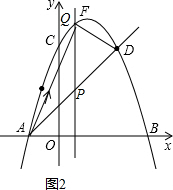
(3)如图2,过Q作QP∥y轴,交直线AD于P,
则Q(x,-x2+2x+3),P(x,x+1),
∴PQ=-x2+2x+3-x-1=-x2+x+2,
∵点A、D分别到直线PQ的距离和为3,
∴S△AQD=S△AQP+S△DQP=$\frac{1}{2}$PQ×3=$\frac{1}{2}$×(-x2+x+2)×3=-$\frac{3}{2}$x2+$\frac{3}{2}$x+3=-$\frac{3}{2}$(x-$\frac{1}{2}$)2+$\frac{27}{8}$,
∴当x=$\frac{1}{2}$时,S△AQD=$\frac{27}{8}$最大,
此时Q纵坐标为$\frac{15}{4}$,即Q点坐标为($\frac{1}{2}$,$\frac{15}{4}$).
点评 此题主要考查了二次函数综合以及三角形面积求法以及二次函数最值求法,正确表示出△AQD的面积是解题关键.

 阅读快车系列答案
阅读快车系列答案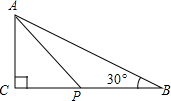 如图,△ABC中,∠C=90°,AB=6,∠B=30°,点P是BC边上的动点,AP的长不可能是( )
如图,△ABC中,∠C=90°,AB=6,∠B=30°,点P是BC边上的动点,AP的长不可能是( )| A. | 2.5 | B. | 4.2 | C. | 5.8 | D. | 3.6 |
| A. | 0.37×105 | B. | 3.7×104 | C. | 37×103 | D. | 370×102 |
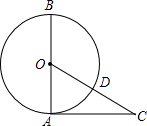 如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)
如图,AB是⊙O的直径,AC是⊙O的切线,OC交⊙O于点D,若∠C=40°,OA=9,则$\widehat{BD}$的长为$\frac{13}{2}$π.(结果保留π)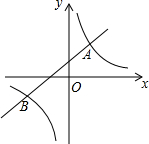 如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.
如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.