题目内容
5．
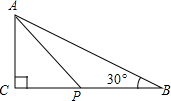如图，△ABC中，∠C=90°，AB=6，∠B=30°，点P是BC边上的动点，AP的长不可能是（ ）| A． | 2.5 | B． | 4.2 | C． | 5.8 | D． | 3.6 |
分析 根据直角三角形30°角所对的直角边等于斜边的一半求出AC，再根据垂线段最短求出AP的最小值，然后得到AP的取值范围，从而得解．
解答 解：∵∠C=90°，AB=6，∠B=30°，
∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3，
∵点P是BC边上的动点，
∴3＜AP＜6，
∴AP的值不可能是2.5．
故选A．
点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，垂线段最短，熟记性质并求出AP的取值范围是解题的关键．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
16．若a＜b，则下列各式中一定成立的是（ ）
| A． | ac＜bc | B． | a2＜b2 | C． | a+1＜b+1 | D． | $\frac{a}{3}$＞$\frac{b}{3}$ |
如图所示，?ABCD的周长为20cm，AE⊥BC于点E，AF⊥CD于点F，AE：AF=2：3，∠C=120°，则?ABCD的面积为24cm2．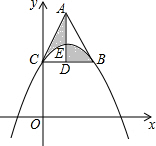
如图，在平面直角坐标系中，点C是抛物线y=a（x-3）2+k与y轴的交点，点B是这条抛物线上另一点，且BC∥x轴，以CB为边向上作等边三角形ABC，BC边上的高AD交抛物线于点E，则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$．
如图，在等腰直角三角形ABC中，∠ACB=90°，AB=4，以点A为圆心，AC长为半径作弧，交AB于点D，则图中阴影部分面积为4-π．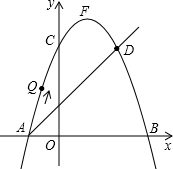
如图，在平面直角坐标系中，直线AD与抛物线y=-x2+bx+c交于A（-1，0）和D（2，3）两点，点C、F分别为该抛物线与y轴的交点和顶点．
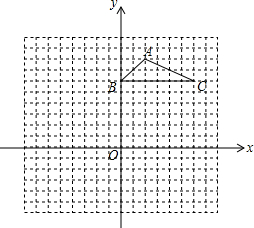如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立如图所示的平面直角坐标系．