题目内容
16．某校八年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛预赛，各参赛选手的成绩如下：八（1）班：88，91，92，93，93，93，94，98，98，100
八（2）班：89，93，93，93，95，96，96，98，98，99
通过整理，得到数据分析表如下：
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| A班 | 100 | 94 | b | 93 | c |
| B班 | 99 | a | 95.5 | 93 | 8.4 |
（2）依据数据分析表，有人说：“最高分在八（1）班，八（1）班的成绩比八（2）班好”，但也有人说八（2）班的成绩要好，请给出两条支持八（2）班成绩好的理由．
分析 （1）利用平均数，中位数，以及方差的定义计算所求即可；
（2）从平均分，以及中位数角度考虑，合理即可．
解答 解：（1）八（2）班的平均分a=$\frac{1}{10}$×（89+93+93+93+95+96+96+98+98+99）=95；
八（1）班的中位数b=93；
八（1）班的方差c=$\frac{1}{10}$×[（88-94）2+（91-94）2+（92-94）2+（93-94）2+（93-94）2+（93-94）2+（94-94）2+（998-94）2+（98-94）2+（100-94）2]=12；
故答案为：95；93；12；
（2）八（2）班的平均分高于八（1）班；八（2）班的成绩集中在中上游，故支持八（2）班成绩好．
点评 此题考查了方差，算术平均数，中位数，以及众数，熟练掌握各自的性质是解本题的关键．
练习册系列答案
相关题目
如图，P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，E、F分别为垂足．
7．中考前的模拟考试对于学生来说具有重大的指导意义，现抽取m名学生的数学一模成绩进行整理分组，形成如下表格（x代表成绩，规定x＞140为优秀），并绘制出扇形统计图和频数分布直方图（横坐标表示成绩，单位：分）．
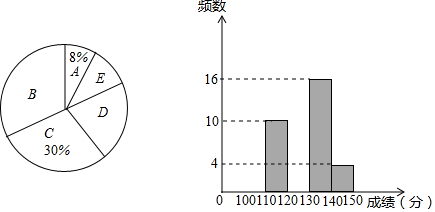
（1）m的值为50；扇形统计图中D组对应的圆心角是72°．
（2）若要从成绩优秀的学生甲、乙、丙、丁中，随机选出2人介绍经验，求甲、乙两人中至少有1人被选中的概率（通过画树状图或列表法进行分析）．
| A组 | 140＜x≤150 |
| B组 | 130＜x≤140 |
| C组 | 120＜x≤130 |
| D组 | 110＜x≤120 |
| E组 | 100＜x≤110 |
（1）m的值为50；扇形统计图中D组对应的圆心角是72°．
（2）若要从成绩优秀的学生甲、乙、丙、丁中，随机选出2人介绍经验，求甲、乙两人中至少有1人被选中的概率（通过画树状图或列表法进行分析）．
已知关于x的不等式3x+mx＞-8的解集如图所示，则m的值为1．
如图，在五边形ABCDE中，AP平分∠EAB，BP平分∠ABC．