题目内容
11.小张去书店购买图书,看好书店有A,B,C三种不同价格的图书,分别是A种图书每本1元,B种图书每本2元,C种图书每本5元.(1)若小张同时购买A,C两种不同图书的6本,用去18元,求购买两种图书的本数;
(2)若小张同时购买两种不同的图书10本,用去18元,请你设计他的购书方案;
(3)若小张同时购进A,B,C三种不同图书10本,用去18元,请你设计他的购买方案.
分析 (1)设小张购买A种图书x本,则购买C种图书(6-x)本,根据购买A,C两种不同图书一共用去18元列出方程,求解即可;
(2)因为书店有A,B,C三种不同价格的图书,而小张同时购买两种不同的图书,所以要将A,B,C两两组合,分三种情况:A,B;A,C;B,C,每种情况都可以根据下面两个相等关系列出方程,两种不同价格的图书本数之和=10,购买两种不同价格的图书钱数之和=18,然后根据实际含义确定他们的解;
(3)有两个等量关系:A种图书本数+B种图书本数+C种图书本数=10,购买A种图书钱数+购买B种图书钱数+购买C种图书钱数=18.设两个未知数,得出二元一次方程,根据实际含义确定解.
解答 解:(1)设小张购买A种图书x本,则购买C种图书(6-x)本.
根据题意,得x+5(6-x)=18,
解得x=3,
则6-x=3.
答:小张购买A种图书3本,购买C种图书3本;
(2)分三种情况讨论:
①设购买A种图书y本,则购买B种图书(10-y)本.
根据题意,得y+2(10-y)=18,
解得y=2,
则10-y=8;
②设购买A种图书y本,则购买C种图书(10-y)本.
根据题意,得y+5(10-y)=18,
解得y=8,
则10-y=2;
③设购买B种图书y本,则购买C种图书(10-y)本.
根据题意,得2y+5(10-y)=18,
解得y=$\frac{32}{3}$,
则10-y=-$\frac{2}{3}$,不合题意舍去.
综上所述,小张共有2种购书方案:
方案一:购买A种图书2本,购买B种图书8本;
方案二:购买A种图书8本,购买C种图书2本;
(3)设购买A种图书m本,购买B种图书n本,则购买C种图书(10-m-n)本.
根据题意,得m+2n+5(10-m-n)=18,
整理,得4m+3n=32,
∵m、n都是正整数,0<4m<32,
∴0<m<8,
将m=1,2,3,4,5,6,7分别代入,仅当m=5时,n为整数,n=4,
∴m=5,n=4,10-m-n=1.
答:小张的购书方案为:购买A种图书5本,购买B种图书4本,购买C种图书1本.
点评 本题考查了一元一次方程、二元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.要注意题中未知数的取值必须符合实际意义.

 备战中考寒假系列答案
备战中考寒假系列答案八(1)班:88,91,92,93,93,93,94,98,98,100
八(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| A班 | 100 | 94 | b | 93 | c |
| B班 | 99 | a | 95.5 | 93 | 8.4 |
(2)依据数据分析表,有人说:“最高分在八(1)班,八(1)班的成绩比八(2)班好”,但也有人说八(2)班的成绩要好,请给出两条支持八(2)班成绩好的理由.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | 1 | 0 | … |
 如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.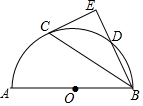 如图,点D是以AB为直径的半圆O上一点,连接BD,点C是$\widehat{AD}$的中点,过点C作直线BD的垂线,垂足为点E.
如图,点D是以AB为直径的半圆O上一点,连接BD,点C是$\widehat{AD}$的中点,过点C作直线BD的垂线,垂足为点E. 已知抛物线c1的顶点为A(-1,4),与y轴的交点为D(0,3).
已知抛物线c1的顶点为A(-1,4),与y轴的交点为D(0,3).