题目内容
14.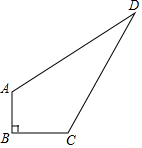 如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
分析 连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出△ACD是直角三角形,分别求出△ABC和△ACD的面积,即可得出答案.
解答  解:连结AC,
解:连结AC,
在△ABC中,
∵∠B=90°,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×3×4=6,
在△ACD中,
∵AD=13,AC=5,CD=12,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴S△ACD=$\frac{1}{2}$AC•CD=$\frac{1}{2}$×5×12=30.
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36.
点评 本题考查了勾股定理,勾股定理的逆定理的应用,解此题的关键是能求出△ABC和△CAD的面积,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
相关题目
16. 一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
 一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )| A. | “年”在下面 | B. | “祝”在后面 | C. | “新”在左边 | D. | “快”在左边 |
17.一元二次方程m1x2+$\frac{1}{3}$x+1=0的两根分别为x1,x2,一元二次方程m2x2+$\frac{1}{3}$x+1=0的两根为x3,x4,若x1<x3<x4<x2<0,则m1,m2的大小关系为( )
| A. | 0>m1>m2 | B. | 0>m2>m1 | C. | m2>m1>0 | D. | m1>m2>0 |
9.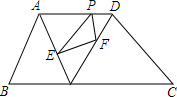 已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
 已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
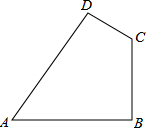 如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补. 如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF=$\sqrt{39}$.
如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF=$\sqrt{39}$. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为$\frac{4}{7}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为$\frac{4}{7}$.