题目内容
2.已知x,y,z均为非负数,且满足x=y+z-1=4-y-2z.(1)用x表示y,z;
(2)求u=2x2-2y+z的最小值.
分析 (1)①×2+②消去z得用x表示y得式子,①+②消去y得用x表示z的式子;
(2)把(1)中求得的式子代入u=2x2-2y+z,得到关于x的二次函数,再根据x、y、z都是非负数列出不等式组求出x的取值范围,然后求出二次函数的对称轴并利用二次函数的增减性解答.
解答 解:(1)解$\left\{\begin{array}{l}{x=y+z-1①}\\{x=4-y-2z②}\end{array}\right.$,
①×2+②消去z得y=3x-2,
①+②消去y得z=-2x+3;
(2)∵x,y,z均为非负数,
∴$\left\{\begin{array}{l}{3x-2≥0①}\\{-2x+3≥0②}\end{array}\right.$,
解不等式①得,x≥$\frac{2}{3}$,
解不等式②得,x≤$\frac{3}{2}$,
∴$\frac{2}{3}$≤x≤$\frac{3}{2}$,
u=2x2-2y-z,
=2x2-2(3x-2)-(3-2x),
=2x2-4x+1,
=2(x-1)2-1,
当x=1时有最小值为2(1-1)2-1=-1.
点评 本题考查了二次函数的最值问题,用x表示出y、z从而得到关于x的二次函数是解题的关键,要注意x的取值范围的求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
4.一名射击运动员,射靶10次,射击成绩分别为(单位:环):9,10,8,7,7,8,9,10,9,8,则他射中9环及9环以上的频率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6.
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6.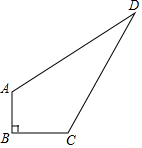 如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积. 如图,AB是⊙O的直径,C,D在⊙O上,CD=AD,分别延长CD、BA相交于点E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半径.
如图,AB是⊙O的直径,C,D在⊙O上,CD=AD,分别延长CD、BA相交于点E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半径.