题目内容
9.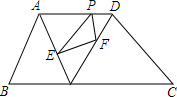 已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )
已知,在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连结AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.则△PEF面积的最大值是( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
分析 设PD=x,S△PEF=y.根据平行线的性质、全等三角形的判定及相似三角形的判定,证明△PEF≌△QFE、△AEP∽△AQD、△PDF∽△ADQ,相似三角形的面积比是相似比的平方,再由三角形AQD与梯形ABCD的面积公式求得梯形的高,代入S△PEF=(S△AQD-S△DPF-S△APE)÷2,得出关于x的二次函数方程,根据顶点坐标公式,求得则△PEF面积最大值.
解答 解:设PD=x,S△PEF=y,S△AQD=z,梯形ABCD的高为h,
∵AD=3,BC=4,梯形ABCD面积为7,
∴$\left\{\begin{array}{l}{z=\frac{1}{2}×3×h}\\{7=\frac{1}{2}×(3+4)h}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{h=2}\\{z=3}\end{array}\right.$,
∵PE∥DQ,
∴∠PEF=∠QFE,∠EPF=∠PFD,
又∵PF∥AQ,
∴∠PFD=∠EQF,
∴∠EPF=∠EQF,
∵EF=FE,
∴△PEF≌△QFE(AAS),
∵PE∥DQ,
∴△AEP∽△AQD,
同理,△DPF∽△DAQ,
∴$\frac{{S}_{△AEP}}{{S}_{△AQD}}$=($\frac{3-x}{3}$)2,$\frac{{{S}_{△}}_{DPF}}{{S}_{△DAQ}}$=($\frac{x}{3}$)2,
∵S△AQD=3,
∴S△DPF=$\frac{1}{3}$x2,S△APE=$\frac{1}{3}$(3-x)2,
∴S△PEF=(S△AQD-S△DPF-S△APE)÷2,
∴y=[3-$\frac{1}{3}$x2-$\frac{1}{3}$(3-x)2]×$\frac{1}{2}$=-$\frac{1}{3}$x2+x,
∵y最大值=$\frac{0-{1}^{2}}{4×(-\frac{1}{3})}$=$\frac{3}{4}$,即y最大值=$\frac{3}{4}$.
∴△PEF面积最大值是$\frac{3}{4}$,
故选:D.
点评 本题综合考查了二次函数的最值、三角形的面积、梯形的面积以及相似三角形的判定与性质,熟练掌握相似三角形的判定与性质及用含x的代数式表示出三角形的面积是解题的关键.

 如图,OD、OE分别为∠AOC、∠COB的平分线,则∠AOB和∠DOE的关系是( )
如图,OD、OE分别为∠AOC、∠COB的平分线,则∠AOB和∠DOE的关系是( )| A. | $\frac{1}{3}$∠AOB=∠DOE | B. | ∠AOB=2∠DOE | C. | 互补 | D. | 互余 |
| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 | 从未听说 |
| 频数 | 40 | 60 | 48 | 36 | 16 |
| 频率 | 0.2 | m | 0.24 | 0.18 | 0.08 |
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.
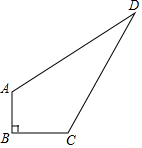 如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积. 数学活动课上,同学们正在讨论一道习题:
数学活动课上,同学们正在讨论一道习题: 如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.
如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.