题目内容
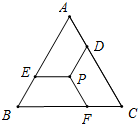 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.
如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.(1)求PD:AB的值;
(2)若AB=12,求PD+PE+PF的值.
考点:三角形的重心,等边三角形的性质
专题:
分析:(1)如图,作辅助线,通过△DPG∽△ABG,列出比例式即可解决问题;
(2)由(1)知:PD:AB=1:3,AB=12,可求出PD=4;同理可求:PE=PF=4,问题即可解决.
(2)由(1)知:PD:AB=1:3,AB=12,可求出PD=4;同理可求:PE=PF=4,问题即可解决.
解答: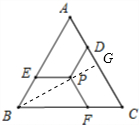 解:(1)连结并延长BP,交AC于G;连接AP;
解:(1)连结并延长BP,交AC于G;连接AP;
∵△ABC为等边三角形,P为重心,
∴BP=2GP,BG=3GP;
∵PD∥AB,
∴△DPG∽△ABG,
∴DP:AB=PG:BG=1:3,
即PD:AB的值为1:3.
(2)∵PD:AB=1:3,且AB=12,
∴PD=4;
同理可求:PE=PF=4,
∴PD+PE+PF=AB=12.
 解:(1)连结并延长BP,交AC于G;连接AP;
解:(1)连结并延长BP,交AC于G;连接AP;∵△ABC为等边三角形,P为重心,
∴BP=2GP,BG=3GP;
∵PD∥AB,
∴△DPG∽△ABG,
∴DP:AB=PG:BG=1:3,
即PD:AB的值为1:3.
(2)∵PD:AB=1:3,且AB=12,
∴PD=4;
同理可求:PE=PF=4,
∴PD+PE+PF=AB=12.
点评:该命题主要考查了三角形的重心及其应用问题;解题的关键是作辅助线,构造相似三角形;灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
小惠在纸上画了一条数轴后,折叠纸面,使数轴上表示1的点与表示-3的点重合,若数轴上A、B两点之间的距离为2014(A在B的左侧),且A、B两点经上述折叠后重合,则A点表示的数为( )
| A、-1006 |
| B、-1007 |
| C、-1008 |
| D、-1009 |
 如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则cosB的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 已知AB=AC,AD=AE,BD=CE,求证:∠ADE=∠EAC+∠ECA.
已知AB=AC,AD=AE,BD=CE,求证:∠ADE=∠EAC+∠ECA. 如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.
如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.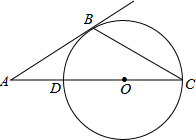 如图,AC经过圆心O交⊙O于点D,AB与⊙O相切于点B.若∠A=x(0°<x<90°)∠C=y,则y与x之间的函数关系图象是( )
如图,AC经过圆心O交⊙O于点D,AB与⊙O相切于点B.若∠A=x(0°<x<90°)∠C=y,则y与x之间的函数关系图象是( )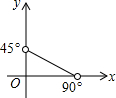


 如图,直线l1:y=
如图,直线l1:y= 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推