题目内容
 如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.
如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.考点:全等三角形的判定与性质
专题:证明题
分析:连接AC,延长DE到F,使EF=BC,连接AF,易证△ABC≌△AEF,进而可以证明△ACD≌△AFD,可得∠ADC=∠ADF即可解题.
解答:解:连接AC,延长DE到F,使EF=BC,连接AF,

∵BC+DE=CD,EF+DE=DF,
∴CD=FD,
∵∠ABC+∠AED=180°,∠AEF+∠AED=180°,
∴∠ABC=∠AEF,
在△ABC和△AEF中,
,
∴△ABC≌△AEF(SAS),
∴AC=AF,
在△ACD和△AFD中,
,
∴△ACD≌△AFD(SSS)
∴∠ADC=∠ADF,
即AD平分∠CDE.

∵BC+DE=CD,EF+DE=DF,
∴CD=FD,
∵∠ABC+∠AED=180°,∠AEF+∠AED=180°,
∴∠ABC=∠AEF,
在△ABC和△AEF中,
|
∴△ABC≌△AEF(SAS),
∴AC=AF,
在△ACD和△AFD中,
|
∴△ACD≌△AFD(SSS)
∴∠ADC=∠ADF,
即AD平分∠CDE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABC≌△AEF是解题的关键.

练习册系列答案
相关题目
下列多项式中,能用公式法进行因式分解的是( )
| A、x2+y2 |
| B、x2-2xy+y2 |
| C、x2+2xy-y2 |
| D、x2+xy+y2 |
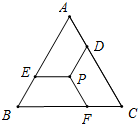 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.
如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.(1)求PD:AB的值;
(2)若AB=12,求PD+PE+PF的值.
在
、-
、-
、
中最大的数是( )
| 1 | |||
|
| 3 | 0.001 |
| 0.01 |
| 1 | ||
-
|
A、
| |||||
B、-
| |||||
C、-
| |||||
D、
|
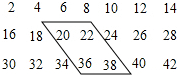 如图是由一些偶数排成的一个数阵.
如图是由一些偶数排成的一个数阵.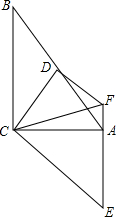 如图,在Rt△ABC中,∠ACB=90°,点D为AB的中点,点E为AC下方一点,AE∥BC且CE⊥CD于点C.
如图,在Rt△ABC中,∠ACB=90°,点D为AB的中点,点E为AC下方一点,AE∥BC且CE⊥CD于点C.