题目内容
 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推(1)第5层所对应的点数是
(2)六边形的点阵共有n层时的总点数是
考点:规律型:图形的变化类
专题:
分析:由于第二层每边有2个点,第三层每边有3个点…,则第二层的六边形点阵的总点数6×2-6=6,第三层的六边形点阵的总点数6×3-6=12,第四层的六边形点阵的总点数6×4-6=18,…,可得到每层总点数等于本层的层数的6倍与6的差,则第n(n>1)层的六边形点阵的总点数6×n-6.
解答:解:第二层的六边形点阵的总点数6×2-6=6,
第三层的六边形点阵的总点数6×3-6=12,
第四层的六边形点阵的总点数6×4-6=18,
…
第n(n>1)层的六边形点阵的总点数6×n-6=6n-6.
当n=5时,6n-6=24,
故答案为,(1)24;(2)6n-6.
第三层的六边形点阵的总点数6×3-6=12,
第四层的六边形点阵的总点数6×4-6=18,
…
第n(n>1)层的六边形点阵的总点数6×n-6=6n-6.
当n=5时,6n-6=24,
故答案为,(1)24;(2)6n-6.
点评:本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
下列多项式中,能用公式法进行因式分解的是( )
| A、x2+y2 |
| B、x2-2xy+y2 |
| C、x2+2xy-y2 |
| D、x2+xy+y2 |
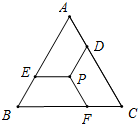 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.
如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.(1)求PD:AB的值;
(2)若AB=12,求PD+PE+PF的值.
正整数排列如图:
第一行 1
第二行 1 2
第三行 2 3 4
第四行 3 4 5 6
按照这样的规律排列,你认为100第一次出现在( )
第一行 1
第二行 1 2
第三行 2 3 4
第四行 3 4 5 6
按照这样的规律排列,你认为100第一次出现在( )
| A、第50行第50个 |
| B、50行第51个 |
| C、第51行第50个 |
| D、第51行51个 |
已知等腰三角形的一边长为3,另一边长为8,则它的周长是( )
| A、14 | B、19 |
| C、11 | D、14或19 |
 已知:如图,AD=BC,∠D=∠C.
已知:如图,AD=BC,∠D=∠C.