题目内容
 如图,直线l1:y=
如图,直线l1:y=| 1 |
| 2 |
| k |
| x |
(1)求双曲线的解析式;
(2)点C在双曲线上,yC=8,求△CBA的面积;
(3)直线l2:y=mx与双曲线相交于P、Q两点(xP>0),当以A、B、P、Q为顶点的四边形的面积等于24时,求点P的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将xA=4代入一次函数解析式求出y的值,确定出A的坐标,将A的坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)过B作y轴的垂线l,过点C、A分别作x轴的垂线,与直线l分别交于点D、E.先将y=
x代入y=
,求出B的坐标,将yC=8代入反比例解析式,求出C点坐标,再由S△CBA=S△CBD+S梯形AEDC-S△ABE,将数值代入计算即可求解;
(3)设P(x,
),即OM=x,PM=
,分四种情况考虑:若P在A的左侧,如图所示,作PM⊥x轴于M,AN⊥x轴于N,由四边形APBQ面积为24,且为平行四边形,得到三角形AOP面积为6,根据三角形POM面积+梯形ANMP面积-三角形AON面积,列出关于x的方程,求出方程的解得到x的值,确定出此时P的坐标;若交点P在第三象限,Q在第一象限,利用对称性求出P的坐标即可;若P在A的右侧,同理可得P的坐标;若交点P在第三象限,Q在第一象限,利用对称性求出P的坐标.
(2)过B作y轴的垂线l,过点C、A分别作x轴的垂线,与直线l分别交于点D、E.先将y=
| 1 |
| 2 |
| 8 |
| x |
(3)设P(x,
| 8 |
| x |
| 8 |
| x |
解答:解:(1)将xA=4代入y=
x=2,即A(4,2),
将A(4,2)代入反比例解析式得:k=8,
所以双曲线的解析式为y=
;
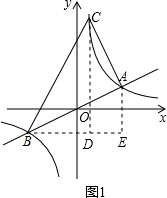 (2)如图1,过B作y轴的垂线l,过点C、A分别作x轴的垂线,与直线l分别交于点D、E.
(2)如图1,过B作y轴的垂线l,过点C、A分别作x轴的垂线,与直线l分别交于点D、E.
将y=
x代入y=
,得
x=
,
解得x=±4,
当x=4时,y=2;当x=-4时,y=-2,
∵A(4,2),
∴B(-4,-2).
将yC=8代入反比例解析式得:x=1,即C(1,8),
∴BD=5,BE=8,CD=10,AE=4.
∴S△CBA=S△CBD+S梯形AEDC-S△ABE=
×5×10+
×(4+10)×3-
×8×4=30;
 (3)设P(x,
(3)设P(x,
),即OM=x,PM=
,
若P在A的左侧,如图2所示,作PM⊥x轴于M,AN⊥x轴于N,
∵由点A、B、P、Q为顶点的四边形面积为24,OP=OQ,OA=OB,即四边形APBQ为平行四边形,
∴S△AOP=S△POM+S梯形ANMP-S△AON=
×24=6,即
x•
+
×(4-x)×(2+
)-4=6,
解得:x=2,即P(2,4);
若交点P在第三象限,Q在第一象限,此时P(-2,-4);
若P在A的右侧,同理可得4+
×(x-4)×(2+
)-4=6,
解得:x=8,此时P坐标为(8,1);
若交点P在第三象限,Q在第一象限,此时P坐标为(-8,-1),
综上,P点坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).
| 1 |
| 2 |
将A(4,2)代入反比例解析式得:k=8,
所以双曲线的解析式为y=
| 8 |
| x |
 (2)如图1,过B作y轴的垂线l,过点C、A分别作x轴的垂线,与直线l分别交于点D、E.
(2)如图1,过B作y轴的垂线l,过点C、A分别作x轴的垂线,与直线l分别交于点D、E.将y=
| 1 |
| 2 |
| 8 |
| x |
| 1 |
| 2 |
| 8 |
| x |
解得x=±4,
当x=4时,y=2;当x=-4时,y=-2,
∵A(4,2),
∴B(-4,-2).
将yC=8代入反比例解析式得:x=1,即C(1,8),
∴BD=5,BE=8,CD=10,AE=4.
∴S△CBA=S△CBD+S梯形AEDC-S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 (3)设P(x,
(3)设P(x,| 8 |
| x |
| 8 |
| x |
若P在A的左侧,如图2所示,作PM⊥x轴于M,AN⊥x轴于N,
∵由点A、B、P、Q为顶点的四边形面积为24,OP=OQ,OA=OB,即四边形APBQ为平行四边形,
∴S△AOP=S△POM+S梯形ANMP-S△AON=
| 1 |
| 4 |
| 1 |
| 2 |
| 8 |
| x |
| 1 |
| 2 |
| 8 |
| x |
解得:x=2,即P(2,4);
若交点P在第三象限,Q在第一象限,此时P(-2,-4);
若P在A的右侧,同理可得4+
| 1 |
| 2 |
| 8 |
| x |
解得:x=8,此时P坐标为(8,1);
若交点P在第三象限,Q在第一象限,此时P坐标为(-8,-1),
综上,P点坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).
点评:此题考查了反比例函数与一次函数的交点问题,坐标与图形性质,三角形、梯形的面积,以及待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
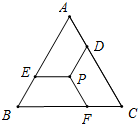 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.
如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.(1)求PD:AB的值;
(2)若AB=12,求PD+PE+PF的值.
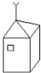 如图所示,从正面看,所能看到的结果是图形( )
如图所示,从正面看,所能看到的结果是图形( )A、 |
B、 |
C、 |
D、 |
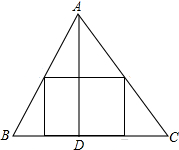 如图,△ABC是一块铁皮,边BC=40cm,高AD=20cm,要用它才出一个矩形铁皮,能否使矩形的周长为48cm?若能,求出裁出矩形铁皮的长和宽;若不能,请说明理由.
如图,△ABC是一块铁皮,边BC=40cm,高AD=20cm,要用它才出一个矩形铁皮,能否使矩形的周长为48cm?若能,求出裁出矩形铁皮的长和宽;若不能,请说明理由.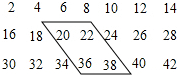 如图是由一些偶数排成的一个数阵.
如图是由一些偶数排成的一个数阵.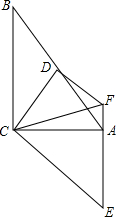 如图,在Rt△ABC中,∠ACB=90°,点D为AB的中点,点E为AC下方一点,AE∥BC且CE⊥CD于点C.
如图,在Rt△ABC中,∠ACB=90°,点D为AB的中点,点E为AC下方一点,AE∥BC且CE⊥CD于点C.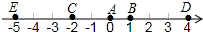 如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样,
如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样,