题目内容
直线y=-x-1与抛物线y=ax2+4ax+b交于x轴上A点和另一点D,抛物线交y轴于C点,且CD∥x轴,求抛物线解析式.
考点:待定系数法求二次函数解析式
专题:
分析:根据直线y=-x-1求得A的坐标,代入抛物线的解析式即可求得b=3a,根据已知可得D的坐标为(-b-1,b)代入抛物线的解析式得出b=a(-b-1)2+4a(-b-1)+b,把b=3a代入得,a(-3a-1)2+4a(-3a-1)=0,分解因式得a(-3a-1)2+4a(-3a-1)=0,即可求得a=0(舍去)或a=1或a=-
,从而求得抛物线的解析式.
| 1 |
| 3 |
解答: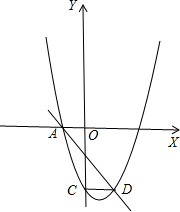 解:如图,∵直线y=-x-1交于x轴上A点,
解:如图,∵直线y=-x-1交于x轴上A点,
∴A(-1,0),
∵抛物线y=ax2+4ax+b交于x轴上A点,
∴a-4a+b=0,
∴b=3a,
由抛物线y=ax2+4ax+b可知C(0,b),
∵CD∥x轴,
∴D的纵坐标为b,
∵点D在直线y=-x-1上,
∴x=-b-1,
∴D(-b-1,b),
∵直线y=-x-1与抛物线y=ax2+4ax+b交于点D
∴b=a(-b-1)2+4a(-b-1)+b,
∴a(-3a-1)2+4a(-3a-1)=0,
即:a(-3a+3a)(-3a-1)=0,
解得:a=0(舍去)或a=1或a=-
,
∴抛物线解析式为y=x2+4x+3或y=-
x2-
x-1.
 解:如图,∵直线y=-x-1交于x轴上A点,
解:如图,∵直线y=-x-1交于x轴上A点,∴A(-1,0),
∵抛物线y=ax2+4ax+b交于x轴上A点,
∴a-4a+b=0,
∴b=3a,
由抛物线y=ax2+4ax+b可知C(0,b),
∵CD∥x轴,
∴D的纵坐标为b,
∵点D在直线y=-x-1上,
∴x=-b-1,
∴D(-b-1,b),
∵直线y=-x-1与抛物线y=ax2+4ax+b交于点D
∴b=a(-b-1)2+4a(-b-1)+b,
∴a(-3a-1)2+4a(-3a-1)=0,
即:a(-3a+3a)(-3a-1)=0,
解得:a=0(舍去)或a=1或a=-
| 1 |
| 3 |
∴抛物线解析式为y=x2+4x+3或y=-
| 1 |
| 3 |
| 3 |
| 4 |
点评:本题考查了直线和抛物线的交点坐标,以及待定系数法求二次函数的解析式,根据已知求得D的坐标是关键.

练习册系列答案
相关题目
 a、b在数轴上对应的点如图所示:
a、b在数轴上对应的点如图所示: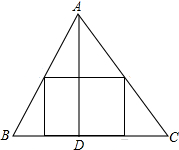 如图,△ABC是一块铁皮,边BC=40cm,高AD=20cm,要用它才出一个矩形铁皮,能否使矩形的周长为48cm?若能,求出裁出矩形铁皮的长和宽;若不能,请说明理由.
如图,△ABC是一块铁皮,边BC=40cm,高AD=20cm,要用它才出一个矩形铁皮,能否使矩形的周长为48cm?若能,求出裁出矩形铁皮的长和宽;若不能,请说明理由.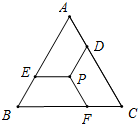 如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.
如图,在等边三角形ABC中,P是△ABC的重心,过点P作PD∥AB,PE∥BC,PF∥AC,分别交AC,AB,BC,于点D,E,F.