题目内容
5.关于x的方程x2-4x+4a=0有两个实数根,则a的取值范围是( )| A. | a<1 | B. | a>1 | C. | a≤1 | D. | a≥1 |
分析 由方程有两个实数根,得到根的判别式大于等于0,即可确定出a的范围.
解答 解:∵关于x的方程x2-4x+4a=0有两个实数根,
∴△=16-4×4a≥0,
解得:a≤1,
故选C.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
15.甲、乙两名射击运动员在某场测试中各射击20次,甲、乙两人的测试成绩如下表,则测度成绩比较稳定的是( )
| 甲的成绩 | 乙的成绩 | ||||||||||
| 环数 | 6 | 7 | 8 | 9 | 10 | 环数 | 6 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 5 | 4 | 5 | 3 | 频数 | 5 | 3 | 4 | 3 | 5 |
| A. | 甲 | B. | 乙 | ||
| C. | 甲、乙两人成绩稳定程度相同 | D. | 无法确定 |
13. 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )
 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
14. 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )| A. | △ADC∽△ACB | B. | △BDC∽△BCA | C. | △ADC∽△CBD | D. | 无法判断 |
 如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,
如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,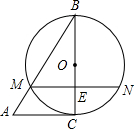 如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.
如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.