题目内容
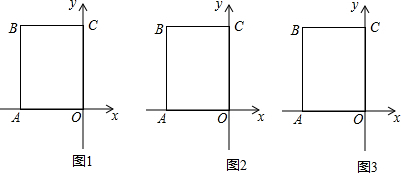
6.如图,在平面直角坐标系中,点A在x轴的负半轴上,其坐标为(-6,0),点C在y轴的正半轴上,其坐标为(0,8),分别过点A、C作y轴的平行线,两平行线相交于点D(1)点B坐标为(-6,8);
(2)动点P从点B出发,以每秒2个单位长度的速度沿折线B-A-O匀速移动,设点P移动的时间为t秒,用含t的式子表示P点坐标;
(3)在(2)的条件下,连接AC、CP,求t为何值时,△ACP的面积与长方形OABC的面积比为1:4,并求出此时点P的坐标.
分析 (1)根据矩形的性质求出点B坐标;
(2)分点P在AB上和点P在AO上两种情况,根据题意计算;
(3)分点P在AB上和点P在AO上两种情况,根据三角形的面积公式计算即可.
解答 解:(1)∵点A的坐标为(-6,0),点C的坐标为(0,8),
∴OA=6,OB=8,
∴点B坐标为(-6,8)
故答案为:(-6,8);
(2)当点P在AB上时,BP=2t,
则AP=8-2t,
∴P点坐标为(-6,8-2t),
当点P在AO上时,BA+AP=2t,
则PO=14-2t,
∴P点坐标为(-14+2t,0);
(3)长方形OABC的面积为6×8=48,
∵△ACP的面积与长方形OABC的面积比为1:4,
∴△ACP的面积为12,
当点P在AB上时,$\frac{1}{2}$×(8-2t)×6=12,
解得,t=2,
此时点P的坐标为(-6,4),
当点P在AO上时,$\frac{1}{2}$×(2t-8)×8=12,
解得,t=5.5,
此时点P的坐标为(-3,0),
则t为2或5.5时,△ACP的面积与长方形OABC的面积比为1:4.
点评 本题考查的是矩形的性质、三角形的面积公式,掌握矩形的性质、灵活运用数形结合思想是解题的关键.

练习册系列答案
相关题目
13.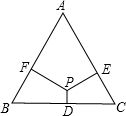 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
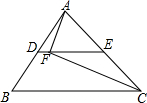 如图,在△ABC中,D,E分别是AB,AC的中点,AC=20,F是DE上一点,连接AF,CF,DF=4.若∠AFC=90°,则BC的长度为( )
如图,在△ABC中,D,E分别是AB,AC的中点,AC=20,F是DE上一点,连接AF,CF,DF=4.若∠AFC=90°,则BC的长度为( ) 如图,在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$.
如图,在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$.
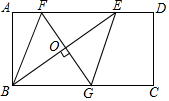 如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.
如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.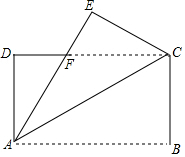 如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.
如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.