题目内容
1. 如图,在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$.
如图,在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$.(1)求BC的长;
(2)如果有一个正方形的边在AB上,另外两个顶点分别在AC、BC上,求这个正方形的面积.
分析 (1)根据勾股定理可求出BD与CD的长度,然后即可求出BC的长度.
(2)由(1)可知△ABC是直角三角形,其中∠BAC=90°,由题意可画出正方形EFGA,求出边长的值即可求出答案.
解答 解:(1)在Rt△ABD中,
由勾股定理可求得:BD=$\sqrt{3}$,
在Rt△ACD中,
由勾股定理可求得:CD=1,
(2)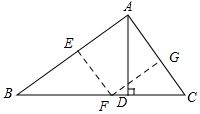 由(1)可知:∠B=∠DAC=30°,
由(1)可知:∠B=∠DAC=30°,
∴∠BAC=90°,
∵一个正方形的边在AB上,另外两个顶点分别在AC、BC上,
∴四边形AEFG是正方形,如图所示,
设AE=EF=x,
∴BE=2$\sqrt{3}$-x,
∵∠B=30°,
∴tan30°=$\frac{EF}{BE}$
∴x=$\frac{\sqrt{3}}{3}$(2$\sqrt{3}$-x)
解得:x=3-$\sqrt{3}$,
∴正方形的面积为:(3-$\sqrt{3}$)2=12-6$\sqrt{3}$
点评 本题考查正方形的性质,解题的关键是求出△BAC是直角三角形,本题属于中等题型.

练习册系列答案
相关题目
9.抽查的甲、乙两班部分学生的视力,记录如下:
(1)求两组数据的平均数,众数,中位数.
(2)比较两组数据的特征,谈谈对“极端值”的认识.
| 甲班 | 0.1 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
| 乙班 | 0.8 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
(2)比较两组数据的特征,谈谈对“极端值”的认识.
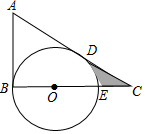 如图,在△ABC中,∠ABC=90°,E是BC上的一点,以BE为直径的⊙O与AC相切于点D,∠A=60°,⊙O的半径为2,则阴影部分的面积2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)
如图,在△ABC中,∠ABC=90°,E是BC上的一点,以BE为直径的⊙O与AC相切于点D,∠A=60°,⊙O的半径为2,则阴影部分的面积2$\sqrt{3}$-$\frac{2}{3}$π.(结果保留根号和π)