题目内容
18.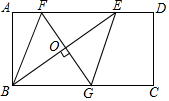 如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.
如图,在矩形ABCD中,E是AD边上一点,连接BE,作BE的垂直平分线分别交AD、BC于点F,G,FG与BE的交点为O,连按BF和EG,试判断四边形BFEG的形状,并说明理由.
分析 根据垂直平分线的性质求出OB=OE,BF=EF,根据矩形性质和平行线性质求出∠FEO=∠GBO,证△FOE≌△GOB,推出OF=OG,即可得出答案;
解答 解:四边形BFEG的形状是菱形,
理由是:∵BE的垂直平分线分别交AD、BC于点F、G,
∴OB=OE,BF=EF,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FEO=∠GBO,
在△FOE和△GOB中,$\left\{\begin{array}{l}{∠FEO=∠GBO}&{\;}\\{OE=OB}&{\;}\\{∠FOE=∠GOB}&{\;}\end{array}\right.$,
∴△FOE≌△GOB,
∴OF=OG,
∵OB=OE,
∴四边形BFEG是平行四边形,
∵BF=EF,
∴四边形BFEG是菱形.
点评 本题考查了矩形的性质,垂直平分线性质,平行四边形的判定,勾股定理,菱形的判定的应用,能综合运用定理进行推理和计算是解此题的关键,综合性比较强,难度偏大.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.抽查的甲、乙两班部分学生的视力,记录如下:
(1)求两组数据的平均数,众数,中位数.
(2)比较两组数据的特征,谈谈对“极端值”的认识.
| 甲班 | 0.1 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
| 乙班 | 0.8 | 0.9 | 1.0 | 1.1 | 1.1 | 1.3 | 1.5 |
(2)比较两组数据的特征,谈谈对“极端值”的认识.
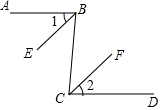 填写下面证明过程中的推理依据:
填写下面证明过程中的推理依据: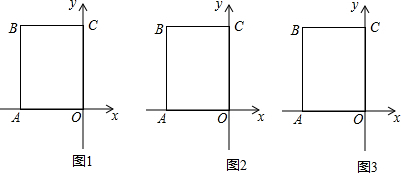
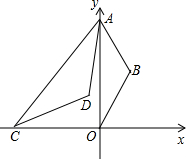 如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.
如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.