题目内容
16．
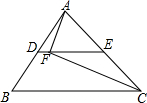如图，在△ABC中，D，E分别是AB，AC的中点，AC=20，F是DE上一点，连接AF，CF，DF=4．若∠AFC=90°，则BC的长度为（ ）| A． | 24 | B． | 28 | C． | 20 | D． | 12 |
分析 如图，首先证明EF=10，继而得到DE=6；再证明DE为△ABC的中位线，即可解决问题．
解答 解：如图，∵∠AFC=90°，AE=CE，AC=20，
∴EF=$\frac{1}{2}$AC=10，
又DF=4，
∴DE=4+10=14；
∵D，E分别是AB，AC的中点，
∴DE为△ABC的中位线，
∴BC=2DE=28，
故选：B．
点评 本题主要考查了三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题；牢固掌握三角形的中位线定理、直角三角形的性质等几何知识点是解题的基础和关键．
练习册系列答案
阅读快车系列答案
相关题目
1．已知关于x的不等式（2-a）x＞1的解集是x＜$\frac{1}{2-a}$；则a的取值范围是（ ）
| A． | a＞0 | B． | a＜0 | C． | a＜2 | D． | a＞2 |
填写下面证明过程中的推理依据：
5．
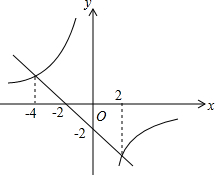若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示，则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为（ ）
若一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象如图所示，则关于x的不等式kx+b-$\frac{m}{x}$≤-2的解集为（ ）| A． | 0＜x≤2或x≤-4 | B． | -4≤x＜0或x≥2 | C． | $-2\sqrt{2}$≤x＜0或x$≥2\sqrt{2}$ | D． | x$≤-2\sqrt{2}$或0$＜x≤2\sqrt{2}$ |
