题目内容
16.解方程:(1)x2-3x+1=0
(2)x2-3x=0
(3)x2-2x=4.
分析 (1)利用公式法求得方程的解即可;
(2)利用因式分解法求得方程的解即可;
(3)利用配方法求得方程的解即可.
解答 解:(1)x2-3x+1=0
b2-4ac=9-4=5
x=$\frac{3±\sqrt{5}}{2}$
解得:x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$;
(2)x2-3x=0
x(x-3)=0
x=0,x-3=0
解得:x1=0,x2=3;
(3)x2-2x=4
x2-2x+1=5
(x-1)2=5
x-1=±$\sqrt{5}$
解得:x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$.
点评 此题考查了解一元二次方程,掌握解方程的步骤与方法,根据方程的特点,选择适当的方法求得方程的解是关键.

练习册系列答案
相关题目
4.一条开口向上的抛物线的顶点坐标是(-1,2),则它有( )
| A. | 最大值1 | B. | 最大值-1 | C. | 最小值2 | D. | 最小值-2 |
6.七名七年级学生的体重,以48.0kg为标准,把超过标准体重的千克数记为正数,不足的千克数记为负数,将其体重记录如表:
(1)最接近标准体重的学生体重是多少?
(2)最高体重与最低体重相差多少?
(3)按体重的轻重排列时,恰好居中的是哪个学生?
(4)求七名学生的平均体重.
| 学 生 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 与标准体 重之差/kg | -3.0 | +1.5 | +0.8 | -0.5 | +0.2 | +1.2 | +0.5 |
(2)最高体重与最低体重相差多少?
(3)按体重的轻重排列时,恰好居中的是哪个学生?
(4)求七名学生的平均体重.
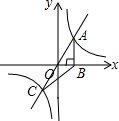 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=6,则反比例函数的解析式为y=$\frac{6}{x}$.
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)与直线y=x交于A、C两点,AB⊥x轴于点B,若S△ABC=6,则反比例函数的解析式为y=$\frac{6}{x}$.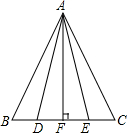 在△ABC中,AB=AC,AF⊥BC,BD=CE,则图中全等三角形共有4对.
在△ABC中,AB=AC,AF⊥BC,BD=CE,则图中全等三角形共有4对.