题目内容
11.解方程组:(1)$\left\{\begin{array}{l}{x+2y=10}\\{y=2x}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x+3y=7}\\{x-3y=8}\end{array}\right.$
(3)$\left\{\begin{array}{l}{\frac{2(x-y)}{3}+1=\frac{x+y}{4}}\\{3(x+y)-2(2x-y)=8}\end{array}\right.$.
分析 (1)利用代入消元法求得方程组的解;
(2)利用加减消元法求得方程组的解;
(3)首先化简方程组,进一步利用加减消元法求得方程组的解.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=10①}\\{y=2x②}\end{array}\right.$
把②代入①得x+2×2x=10.
解得:x=2,
代入②得y=4,
所以原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{2x+3y=7①}\\{x-3y=8②}\end{array}\right.$
①+②得3x=15,
解得:x=5,
代入②得5-3y=8
解得:y=-1,
$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{\frac{2(x-y)}{3}+1=\frac{x+y}{4}}\\{3(x+y)-2(2x-y)=8}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{5x-11y=-12①}\\{-x+5y=8②}\end{array}\right.$,
①+②×5得14y=28,
解得:y=2,
代入②得-x+10=8,
解得:x=2,
所以原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
6.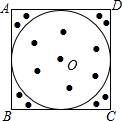 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )| A. | π≈$\frac{a}{b}$ | B. | π≈$\frac{4b}{a}$ | C. | π≈$\frac{b}{a}$ | D. | π≈$\frac{4a}{b}$ |
3.某市商品房的均价原为18150元/m2,经过连续两次降价后均价为15000元/m2.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A. | 18150(1-x)2=18150-15000 | B. | 18150(1-x2)=15000 | ||
| C. | 18150(1-2x)=15000 | D. | 18150(1-x)2=15000 |
1.点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数y=-$\frac{4}{x}$的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是( )
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y2<y3<y1 |
 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2,则顶点A2的坐标是(2,-3).
如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2,则顶点A2的坐标是(2,-3).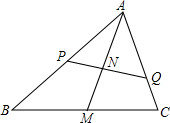 设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.
设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$. 已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.
已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.