题目内容
计算：17×3.14＋61×3.14＋22×3.14；
314
【解析】试题分析：根据提公因式法分解因式，先确定公因式3.14，再提取公因式即可.
试题解析：17×3.14＋61×3.14＋22×3.14
=3.14×（17+61+22）
=3.14×100
=314
练习册系列答案
相关题目
如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗？请说明理由．
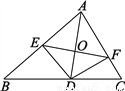
AD是线段EF的垂直平分线，理由见解析
【解析】试题分析：由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论.
试题解析：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠AED=∠AFD=90°，
∴∠DEF=∠DFE，
∴∠AEF=∠AFE，
∴AE=AF，
∴点A、D都在EF的垂直... 若关于x的方程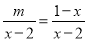
有增根，则m的值为( )
A. 0 B. 1 C. －1 D. 2
C
【解析】试题解析：方程两边同乘以x?2，得
①
∵原方程有增根，
∴x?2=0，
即x=2.
把x=2代入①，得
m=?1.
故选C. 在△ABC中，∠C＝90°，AB＝13，BC＝5，则tanB＝________．
【解析】∵∠C=90°，AB=13，BC=5，∴AC==12，∴tanB=，
故答案为： . 如图，在四边形ABCD中，AD∥BC，AC⊥AB，AD=CD，cos ∠DCA=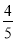
，BC=10，则AB的值是( )
A. 3 B. 6 C. 8 D. 9
B
【解析】∵AD∥BC，∴∠DAC＝∠ACB．∵AD＝CD，
∴∠DAC＝∠DCA．∴∠ACB＝∠DCA．
∴，即，∴AC＝8，
∴． 右图中四边形均为长方形，根据图形，写出一个正确的等式：_____________．
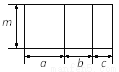
m（a+b+c）=ma+mb+mc（答案不唯一）．
【解析】试题分析：从两方面计算该图形的面积即可求出该等式
本题解析：从整体来计算矩形的面积：m(a+b+c)，
从部分来计算矩形的面积：ma+mb+mc，
所以m(a+b+c)=ma+mb+mc
故答案为：m(a+b+c)=ma+mb+mc 多项式15m3n2+5m2n﹣20m2n3的公因式是（ ）
A. 5mn B. 5m2n2 C. 5m2n D. 5mn2
C
【解析】多项式15n²+5m²n?20m² 中，
各项系数的最大公约数是5，
各项都含有的相同字母是m、n，字母m的指数最低是2，字母n的指数最低是1，
所以它的公因式是5m²n.
故选C. 如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B；求证：CD⊥AB；
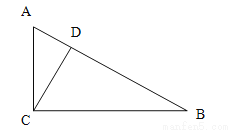
证明过程见解析
【解析】试题分析：根据∠ACB=90°得出∠A+∠B=90°，结合已知条件得出∠A+∠ACD=90°，从而得出答案.
试题解析：∵∠ACB=90° ∴∠A+∠B=90° ∵∠ACD=∠B ∴∠A+∠ACD=90° ∴∠ADC=90°
∴CD⊥AB 要画出某一图形平移后的图形，必须知道_____和_____
方向 距离
【解析】试题解析：平移前后两个图形全等，但是要画出来的话必须知道平移的方向和距离.
故答案为：(1). 方向 (2). 距离.