题目内容
6.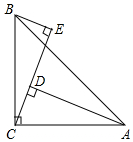 如图,AC=BC,∠ACB=90°,BE⊥CE垂足为E,AD⊥CE垂足为D,AD=5,DE=3,求BE的长.
如图,AC=BC,∠ACB=90°,BE⊥CE垂足为E,AD⊥CE垂足为D,AD=5,DE=3,求BE的长.
分析 可先证明△BCE≌△CAD,可求得CE=AD,结合条件可求得CD,则可求得BE.
解答 解:
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
又∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△CBE和△ACD中,
$\left\{\begin{array}{l}{∠E=∠ADC}\\{∠CBE=∠ACD}\\{BC=AC}\end{array}\right.$
∴△CBE≌△ACD(AAS),
∴BE=CD,CE=AD=5,
∵DE=3,
∴CD=CE-DE=AD-DE=5-3=2,
∴BE=CD=2.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.一个正整数的算术平方根为a,则比这个正整数大3的数的算术平方根是( )
| A. | a+3 | B. | a+$\sqrt{3}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\sqrt{a+3}$ |
14.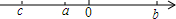 已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c+a|-3|a-b|=( )
已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c+a|-3|a-b|=( )
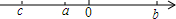 已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c+a|-3|a-b|=( )
已知有理数a,b,c在数轴上对应点的位置如图所示,化简:|b-c|-2|c+a|-3|a-b|=( )| A. | -5a+4b-3c | B. | 5a-2b+c | C. | 5a-2b-3c | D. | a-2b-3c |
15.下列命题中,属于假命题的是( )
| A. | 三角形的内角和等于180° | |
| B. | 对顶角相等 | |
| C. | 圆的任何一条直径都是它的对称轴 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线相互平行 |
 如图所示,在3000个“〇”中依次填入一列数字a1,a2,a3,…a3000,使得其中任意四个相邻“〇”中所填数字之和都等于-10,已知a999=-2x,a25=x-1,可得x的值为2;a2017=1.
如图所示,在3000个“〇”中依次填入一列数字a1,a2,a3,…a3000,使得其中任意四个相邻“〇”中所填数字之和都等于-10,已知a999=-2x,a25=x-1,可得x的值为2;a2017=1.