题目内容
11. 如图所示,在3000个“〇”中依次填入一列数字a1,a2,a3,…a3000,使得其中任意四个相邻“〇”中所填数字之和都等于-10,已知a999=-2x,a25=x-1,可得x的值为2;a2017=1.
如图所示,在3000个“〇”中依次填入一列数字a1,a2,a3,…a3000,使得其中任意四个相邻“〇”中所填数字之和都等于-10,已知a999=-2x,a25=x-1,可得x的值为2;a2017=1.
分析 由于任意四个相邻数之和都是-10得到a1+a2+a3+a4=a2+a3+a4+a5,a5+a6+a7+a8=a6+a7+a8+a9,…,则a1=a5=a9=…=,利用同样的方法可得到a2=a6=a10=…=-7,a3=a7=a11=…,a4=a8=a12=…=0,所以已知a999=a3=-2x,a25=a1=x-1,由此联立方程求得x,进一步求得a2017即可.
解答 解:∵a1+a2+a3+a4=a2+a3+a4+a5,a5+a6+a7+a8=a6+a7+a8+a9,…,
∴a1=a5=a9=…=-2x,
同理可得a2=a6=a10=…=-7,
a3=a7=a11=…=x-1,
a4=a8=a12=…=0,
∵a1+a2+a3+a4=-10,
∴-2x-7+x-1+0=-10,
解得:x=2;
则a2017=a3=1.
故答案为:2,1.
点评 本题考查数字的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.用四舍五入法,把数2.701保留三个有效数字,得到的近似数是( )
| A. | 2.7 | B. | 2.70 | C. | 2.701 | D. | 2.71 |
16.数轴上到-4的距离等于5个单位长度的点表示的数是( )
| A. | 5或-5 | B. | 1 | C. | -9 | D. | 1或-9 |
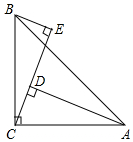 如图,AC=BC,∠ACB=90°,BE⊥CE垂足为E,AD⊥CE垂足为D,AD=5,DE=3,求BE的长.
如图,AC=BC,∠ACB=90°,BE⊥CE垂足为E,AD⊥CE垂足为D,AD=5,DE=3,求BE的长.